9. 三角學 (Trigonometry)
9.2 特殊角的三角比
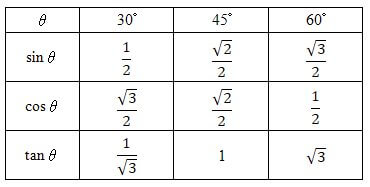
“特殊角的三角比”其實是指“30°、45°、60°”的三角比數值。它們“特殊”是因為它們的三角比的值是帶有根式的簡單分數（如下表所示）：
點去幫助背誦上表
於中三階段，老師大多要求同學背誦上表。我見過一個同學用以下方法背誦：
- 第一行是sin。三角比數值的分母全是２；分子分別是 \(\sqrt{1}(即1)、\sqrt{2}、\sqrt{3}\)。
- 第二行是cos。三角比數值與sin的次序相反。
- 第三行是tan。由 \(\dfrac{1}{\sqrt{3}} \) 開始，每次乘 \(\sqrt{3}\)。
另一方法是利用計數機：
- 先按出要求的三角比值(如sin60°)
- 當顯示的數值“唔靚仔”時，按x2的功能鍵求二次方後的值(這時應顯示出75)
- 按“分數”的功能鍵把小數值化為分數(這時應顯示出3/4)
- 因之前“取了二次方”，所以三角比的值就是把分數的分子、分母開方（即 \( sin60^{\circ} = \dfrac{\sqrt{3}}{\sqrt{4}} = \dfrac{\sqrt{3}}{2} \) ）
9.3 常用的三角恆等式
喺考三角學嘅時候，有一種題目係叫你化簡一個三角比數式。喺依個時候就要用以下嘅三角恆等式。
- \( tan \theta = \dfrac{sin\theta}{cos\theta} \)
- \(sin^{2}\theta + cos^{2}\theta = 1 \)
- \(sin\theta = cos(90^{\circ} – \theta) \)
- \(cos\theta = sin(90^{\circ} – \theta) \)
- \( tan \theta = \dfrac{1}{tan(cos(90^{\circ} – \theta)} \)
例1： 化簡 \( sin\theta tan(90^{\circ} – \theta) \)
解：
\( \begin{align}
sin\theta tan(90^{\circ} – \theta) & = sin \theta \times \dfrac{sin(90^{\circ} – \theta)}{cos(90^{\circ} – \theta)} \\
& = sin \theta \times \dfrac{cos\theta}{sin\theta} \\
& = cos\theta
\end{align}\)