1. 不等式 (Inequalities)
1.1 不等式的意義
簡單來說，不等式是一個表示“不相等關係”的數式。
其實日常生活中都有好多不相等關係的例子：
- 4人的士載乘客的數量細過4
- 爸爸和媽媽的年齡相加大過100
- 旅行社舉辦旅行團時，參加人數必須大於10人才「成行」
1.2 不等號
考慮x和y兩變數，“x不相等y”有四種情況，可能以下四個不等號嚟表示：
- \(x > y \quad \quad x大於y\)
- \(x \geqslant y \quad \quad x大於或等於y\)
- \(x < y \quad \quad x小於y\)
- \(x \leqslant y \quad \quad x小於或等於y\)
留意:
- \(x > y \quad 同\quad y < x quad 嘅意思係一樣的。\)
- 因為 「x大過y」即「y細過x」
- \(x > y \quad 同\quad y < x quad 嘅意思係一樣的。\)
1.3 於數線上用圖像表示不等式
當我地講「x 大過3」嘅時候，咁x可以係幾多呢?可以係4, 5, 5.3, 1000, 999, 9999，總之x嘅值係喺「大過3嘅範圍」入面都可以。
為咗更容易地表逹x可以選取嘅範圍，我地有時會喺數線上用圖像嚟表示可選取嘅範圍。
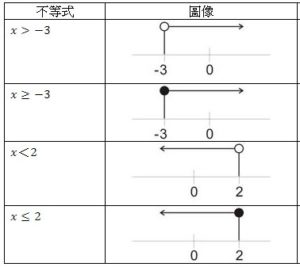
從上面嘅圖像中，大家應不難發現
- 當不等式符號沒有“等於”嘅部份，我們要使用空心圓。
- 當不等式是“大於”時，箭咀指向右邊。咁係因為數線上，𧻗向右數值就𧻗大。
- 相反，當不等式是“大於”時，箭咀指向左邊（－３右邊的數比－３大）。
1.4 不等式的基本性質
- 傳遞性質（Transitive Property）
- 如果 a > b 及 b > c，則 a > c 。
- 加法性質（Additive Property）
- 如果 a > b ，則 a + c > b + c 。
- 乘法性質（Multiplicative Property）
- 如果 a > b 及 c > 0，則 ac > bc 。
- 如果 a > b 及 c < 0，則 ac < bc 。
簡單嚟講，大家只要記住「當對不等式左右同時乘或除一個負數字，個不等式符號要倒轉」就可以了。
- 倒數性質（Reciprocal Property）
- 如果 a > b 且 a、b均是正數，則 \(\dfrac{1}{a} < \dfrac{1}{b}\)
- 如果其中一個係負數，則左右攞倒數後個符號不變。
** 倒數性質喺初中嘅時候大家唔太明都唔緊要。當出現倒數時，大家用數字去想一想就可以了。- 例如 -2 < 5。
攞倒數後係 \(1\dfrac{1}{2} 同 \dfrac{1}{5}\)。因為負數點都係細過正數，所以 \(1\dfrac{1}{2} < \dfrac{1}{5}\)。
- 例如 -2 < 5。