演繹幾何 (Deductive Geometry)

5.1 什麼是演繹幾何

所謂的演繹幾何基本上係利用一些已知的嘅幾何定理(如「三角形內角和」、「直線上的鄰角」)去推論出圖形中另一些未知角的大小(即角係幾多度)。除此之外亦可以係叫你證明一些圖形中的性質(如「證明兩條線係平行的」、「證明某三角形係等腰三角形」)。

喺初中入面，俾你嘅圖主要係由平行線、三角形、多邊形。

喺中一、中二時其實大家已經學晒所有初中要識嘅幾何定理。中三時已係期望大家能融會貫通咁利用不同嘅定理去解答問題。

所以，請同學先溫習：

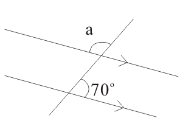例1：求右圖中的未知數a。
解說：

首先我哋最緊要首先睇吓幅圖有咩特別。
好似依幅圖咁，好明顯有一對平行線，所以我哋“九成九”要用“同平行線有關”嘅定理。
- 諗一諗D平行線定理，你會發現冇一個定理可以幫我哋直接求得a。
- 但唔緊要，提示只係提示，我哋要做嘅，係用一次個提示。
- 如果你用“同位角”或者“內錯角”定理，只要求到嗰隻相等嘅角，你就會發現只要再用一次“直線上的鄰角”就可以計到 \(a = 110^{\circ}\)；
- 如果你用“同旁內角”定理，你會發現只要再用一次“對頂角”就可以計到 \(a = 110^{\circ}\)；