8. 坐標幾何 (Coordinate Geometry)
8.1 坐標幾何 – 基礎知識
未開始重溫中三教嘅坐標幾何，建議大家先溫習一吓中一的“坐標簡介”。
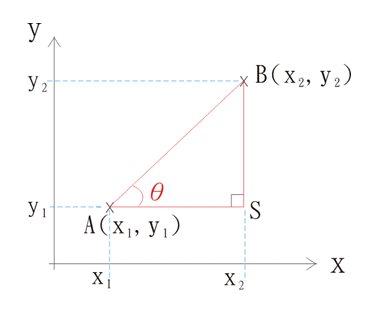此外，喺依課入面，我哋會利用右邊幅圖。
留意圖中有兩點A、B，坐標分別係\((x_{1}, y_{1})\)同\((x_{2}, y_{2})\)。
8.2 兩點間的距離
A、B兩點之間的距離 (或AB線段的長度)可以以下公式計算出來。
\(\quad AB = \sqrt{(x_{2} – x_{1})^{2} + (y_{2} – y_{1})^{2}} \)
如果大家怕記唔到或唔明白條公式，可以參吓下面嘅解釋：
- AS = x2 – x1
- BS = y2 – y1
- AB係直角三角形ABC的斜邊。可用畢氏定理嚟計（即用公式\(a^{2} + b^{2} = c^{2}\)）。
8.3 直線的斜率 (Slope of a straight line)
直線嘅斜率即係代表咗條邊有幾斜同斜向邊一邊。
我哋通常用細楷“m”代表斜率，所以AB的斜率通常會寫成 \(m_{AB}\)（留意AB係細D咁寫喺m嘅右下角）。
\( \quad AB的斜率 = \dfrac{y_{2} – y_{1}}{x_{2} – x_{1}} \)
留意一吓水平線同鉛垂線嘅斜率
- 水平線（即與x-軸平行的線）的斜率是0。
- 咁係因為喺水平線上，AB兩點嘅y坐標會一樣，所以m會等於0。
- 鉛垂線（即與y-軸平行的線）的斜率是沒有意義的。
- 咁係因為喺鉛垂線上，AB兩點嘅x坐標會一樣，所以m會等於「\(\dfrac{y_{2} – y_{1}}{0} \)」,一個數係唔可以被零除的。
8.4 平行線與垂直線 (Parallel lines and Perpendicular lines)
- 若兩條線互相平行，則它們的斜率相等，即 m1 = m2
- 若兩條線互相垂直，則 m1 x m2 = – 1
8.5 分點兩點的中點 (Mid-point of 2 points)
若M點是AB線段上的中間點，則M的坐標(x, y) 可用以下公式計算出來。
\(\quad x = \dfrac{x_{1} + x_{2}}{2} \quad，x = \dfrac{y_{1} + y_{2}}{2} \)
8.6 分點 (Point of Division)
若P點是AB線段上的一點使 AP : PB = r : s，則P點的坐標(x, y)為：
\(\quad x = \dfrac{sx_{1} + rx_{2}}{r + s} \quad，x = \dfrac{sy_{1} + ry_{2}}{r + s} \)