13. 三角形的心 (Centers of Triangles)
13.1 什麼是三角形的心?
三角形的心 是指
- 重心 (Centriod)
- 垂心 (Orthocenter)
- 外心 (Circumcenter)
- 內心 (Incenter)
- 旁心 (不過這個不在課程範圍之內)
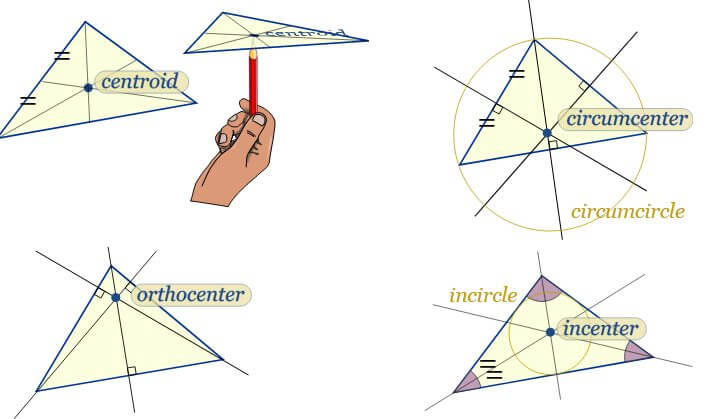
13.2 重心 (Centriod)
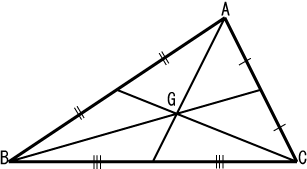
定義：三條中線(median)的交點
- 中線嘅劃法係由三角形的其中一個頂點畫一條線去對邊嘅中心點
特點：
- 理論三角形係點嘅樣都好，重心必定在三角形之內。
- 重心有「重量的中心」。假如我地找到一件物件的重心，理論上可用一枝針支撐住件物件而物件又唔會傾倒。
- 重心定理：重心到頂點的距離是到對邊中點距離的2倍。
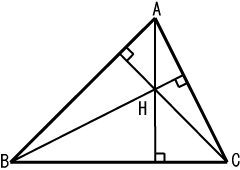
13.2 垂心 (Orthocenter)
定義：三條高線(altitude)的交點
- 高線嘅劃法係由三角形的其中一個頂點畫一條垂直於對邊嘅線
特點：
- 銳角三角形的垂心在三角形內部
- 直角三角形的垂心在三角形的直角頂點
- 鈍角三角形的垂心在三角形的外部。
13.4 外心 (Circumcenter)
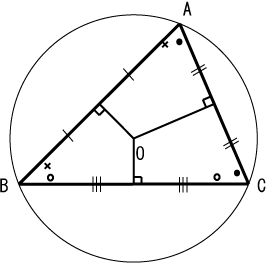
定義：三條邊的垂直平分線(perpendicular bisector)的的交點
- 垂直平分線線嘅劃法係喺由三角形的其中邊上定出中點，然後畫一條垂直線
特點：
- 外心可以在三角形之外。
- 外心為三角形外接圓的圓心。
- 即可以用外心(圖中的O點)為圓心，以OA為半徑畫出一個圓形，而三角形頂點A、B、C皆在圓周上。
- OA=OB=OC=圓半徑
13.5 內心 (Incenter)
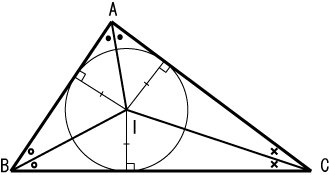
定義：三個內角的角平分線(angle bisector的的交點
- 角平分線係指條線會把一個角分成兩等份。
特點：
- 內心必定在三角形之內。
- 內心為三角形內切圓的圓心
- 可以用內心(圖中的I點)為圓心，再劃一條垂直線到其中一邊，並以此為半徑畫出一個圓形。圓形會剛好掂到其餘兩邊。
- 即圖中的I點與三邊的距離相等，且為內切圓的半徑。
對於數學基礎唔好嘅同學，我認為只需大約睇吓，記到或明到幾多都算。因為一般提及三角形的心嘅題目都會較深。