7. 面積與體積 (Area & Volume)
7.2 棱錐 (Pyramid)
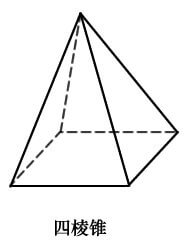棱錐是一個底為多邊形的尖塔。
喺初中問得大家嘅，99%都係正棱錐，即底圖形係一個正多邊形，而個尖頂係喺正個底嘅中心上方。而每個側面都係一樣嘅。
- \( 體積 = \dfrac{1}{3}\times 底面積 \times 高\)
- 總表面面積 = 所有側面的總面積 + 底面積
7.3 圓錐 (Cone)
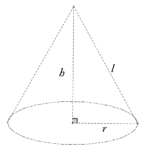圓錐是一個底為圓形的尖塔。
除了高度外，我們還要留意圓錐有一個“斜高”。“斜高”是底部圓周上的一點與頂點的連線的長度。
- 留意 r、h、l 係直角三角形的三邊。而按畢氏定理:
\(\quad r^{2} + h^{2} = l^{2}\) - \( 體積 = \dfrac{1}{3}\times 底面積 \times 高 = \dfrac{1}{3}\pi r^{2}h\)
- \(曲面面積 = \pi \times r \times l \)
- \(總表面面積 ＝ 曲面面積 + 底面積 ＝ \pi r l + p r^{2}\)
7.4 球體
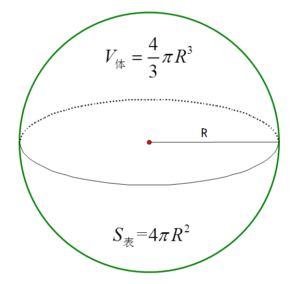球體即係一個波。
- \(體積 = \dfrac{4}{3}\pi r^{3}\)
- \(表面面積 = 4\pi r^{2}\)
7.5 相似形狀
要理解咩係相似形狀，大家只要諗吓叮噹(多啦A夢)嘅變大縮小槍就可以了。
對於兩個相似形狀，如果l1 和 l2 是任何兩條對應邊的長度，則它們的表面面積比（A1 : A2）和體積比( V1：V2)是：
- \(\dfrac{A_{1}}{A_{2}} = \left ( \dfrac{A_{1}}{A_{2}} \right )^{2} \)
- \(\dfrac{V_{1}}{V_{2}} = \left ( \dfrac{A_{1}}{A_{2}} \right )^{3} \)
大家留意有時題目係比咗個面積比你，但就要求你去計體積比。解題嘅技巧係
- 先利用面積比計出個邊長比
- 再利用邊長比計體積比