10. 三角比的應用 (Applications of Trigonometry)
喺日常生活入面，我諗三角比最有用都係喺建築或測量方面。
10.1 斜率與傾角
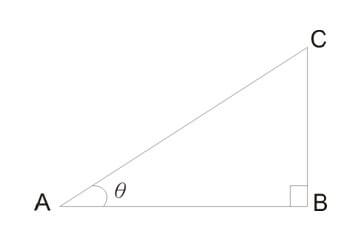斜率與傾角(θ)都是用來表示一個斜坡的傾斜度的。
\(右圖中斜坡AC的斜率 = \dfrac{斜坡的高度}{斜坡的水平長度} = \dfrac{BC}{AB} \)
斜率通常會以“1：n”來表示。
- 如AC的斜率 = 2 / 3，則AC的斜率是“1 : 1.5”(因 2 : 3 = 1 : 1.5)
斜坡AC的傾角 = 斜坡與水平線的夾角 ＝θ
留意： 利用三角比的知識， AC的斜率 = tanθ
10.2 仰角和俯角
- 當我們觀察位於上方的物件時，視線與水平線所形成的角稱為仰角。
- 當我們觀察位於下方的物件時，視線與水平線所形成的角稱為俯角。
10.3 方位
方位是用來表示一個目標是在觀察點的哪一個方向。
通常以“由觀察點A測得目標B的方位是xxxx”來表示。
10.3.1 羅盤方位角 (Compass bearing)
大家都應該知道指南針有以下幾個大方向：
- 東 = E (East)
- 南 = S (South)
- 西 = W (West)
- 北 = N (North)
而羅盤方位角就係基於以上四個大方向，再更細指地描述方向的一種方法。
例1： N30°E
解釋：它的意思是“由北開始，向東轉30度”。
- 北和南作首要方位
- 東和西為次要方位
- 在兩者之間加上角度
- 因此角度只會由 0°至 90°
明白後可以看到一個象限角可分成三部份：
- 第一個部份是開始的方向，只可以是N或S
- 第三個部份是向哪一個方向度起，只可以是E或W
- 第二個部份（即中間的度數）是量度的角度
- 這角度只會由 0°至 90°
例2： 求右圖中，由P測Q的羅𥂟方位角。
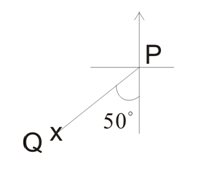
答： 由P測Q的羅𥂟方位角是S50°W。
10.3.2 真方位角 (True bearing)
真方位角是由北作為0°，按順時針方向開始量得的角度。
例3： 在例2中，由P測Q的真方位角是230°。 (因為 180° + 50° = 230° )