12. 統計 (Statistics)
統計又係一個大家每一年都會學嘅課題。其實初中嘅統計都唔係太難， 中二統計 入面主要係要學識點睇圖、點將數據分組同按要求畫個統計圖出嚟。
12.1 頻數多邊形 (Frequency Polygon)
頻數多邊形是一種以折線來表達數據分佈的統計圖。
12.1.1 繪圖方法
- 把原始資料分組列成頻數表
- 以組中點作x軸，頻數作y軸
- 在首尾組中點以外在加上額外兩組頻數為零的組中點以直線連起這些組中點
例1： 以下所示為20人的身高（單位是cm）：
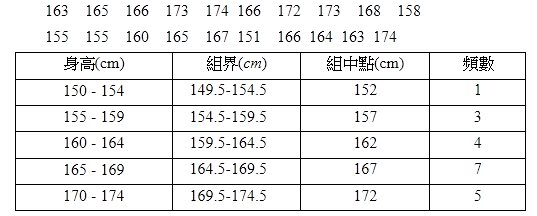
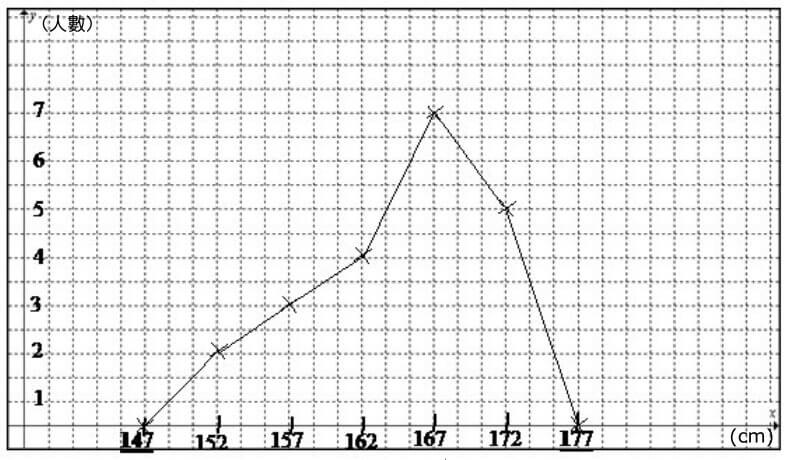
畫圖就係咁簡單! 不過有關分組數據，大家要留意以下詞彙嘅定義:
- 組區間 (Class interval)
指每組數據嘅範圍(range)。 - 組限 (Class limit)
指每個數據組兩個末端的值，包括下組限 (lower class limit)及上組限 (upper class limit)。 - 組中點 (Class mark)
指每個數據組嘅中間值，也可以說是兩個組限嘅平均數。 - 組界 (Class boundary)
分為下組界及上組界。其實只係一個數據組嘅下組界同另一個數據組嘅上組界嘅中間值。 - 組距 (Class width)
上組界與下組界的差。
對150-154 嗰組數據嚟講，
- 組區間 = 150 – 154cm
- 下組限=150cm，上組限=154cm
- 組中點= 152cm
- 下組界 = 149.5cm，上組界 = 154.5cm
- 組距 = 154.5 – 149.5 = 5cm
12.2 累積頻數多邊形 (Cumulative Frequency Polygon)
累積頻數多邊形是一個表示數據的累積頻數變化圖像。
12.2.1 繪圖方法
- 把原始資料分組列成累積頻數表
- 以組界上限作x軸，累積頻數作y軸
- 以直線連起這些組中點
例： 以下所示為20人的身高（單位是cm）：
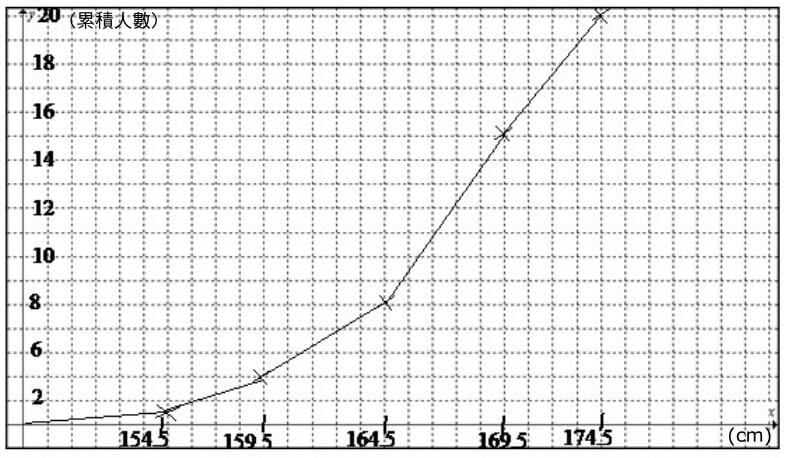
12.2.2 四分位數 (Quartiles)
相信大家都記得統計學上有個「中位數」(即係咗細至大排時，中間嘅數據的值)。
而所謂中嘅中間，我地藉可以話係第50百分數(50%)嘅數據值。如再細分，就會睇第25和75百分位數嘅數據值。而數學家就因此定出以下兩個名詞：
- 上四分位數(upper quartile)
這是累積頻數的第75百分位數的數據值。 - 下四分位數(lower quartile)
這是累積頻數的第25百分位數的數據值。
- 上四分位數(upper quartile)
如覺自己數學基礎唔好，大可重溫一吓中一時學咗咩。請按「中一|統計簡介」