5. 聯立二元一次方程 (Simultaneous Linear Equations)
要了解咩係聯立二元一次方程,其實可以從個名開始。
- 「元」係指變數,而二元方程係指方程中有兩個變數出現。
- 「一次」係指變數嘅次數最高係1。
- 「聯立」係指要同時成立。
我地見睇一個解「一元一次方程」嘅例子。
例1:
\(\begin{align}
\quad \quad 3x + 5 & = 8 \\
3x & = 3 \\
x & = 1
\end{align}\)
假如我比一條「二元一次方程」要你解呢?例如方程係
\(\begin{align}
& \quad \quad x – y = 2 \\
& 你會發現係你計唔到一個”明確”嘅解(即)答案。\\
& 相反,答案係有無限嘅可能性。\\
& 例如「x=3, y=1」、「x=4, y=2」、「x=5, y=3」、「x=7, y=5」等。
\end{align}\)
但如果我比多個限制你,同時要求 x + y = 4呢?咁你會發現除咗「x=3, y=1」之外,其他組合例如「x=4, y=2」、「x=5, y=3」、「x=7, y=5」等都唔會符合我後加嘅方程。因此,我地會話依個聯立方程嘅解係「x=3, y=1」。
由上面嘅例子,你應會發現當有兩個變數嘅時候,要計到一個唯一嘅解係要有兩條方桯嘅。就係依個原因,所以先有「聯立二元一次方程」這一課。
5.1 解聯立方程之方
5.1.1 代入消元法 (Method of Substitution)
代入消元法係指
- 先從其中一條方程,利用主項變換嘅技巧,把其中一個變數寫成主項(即 y = 咩咩咩,或 x = 咩咩咩)
- 再把這關係代入另外一條方程。這樣做的結果是這條方程就只有一個變數。之後就可以利用一般嘅解方程技巧嚟計出變數的答案。
- 最後再把答案代入隨便的一條方程,咁就可以計到另一個變數的答案。
例2: 解以下聯立方程
\(\quad \quad \left\{\begin{matrix}
& x + 2y = 3 \quad && —— (1)\\
& 3x + 2y = 5 \quad && —— (2)
\end{matrix}\right.\)
解:
\(\begin{align}
\quad 從 (1),\quad \quad \quad \\
\quad \quad x & = 3 – 2y \quad \quad —- (3)\\
把 (3) 代入 (2),\\
\quad 3(3 – 2y) + 2y & = 5 \\
9 – 6y + 2y & = 5 \\
-4y & = -4 \\
y & = 1 \\
把 y = 1代入 (3) && \\
x & = 3 – 2(1) = 1 \\
\therefore \quad 方程組的解是& x = 1,y = 1。&&
\end{align}\)
5.1.2 加減消元法 (Method of Elimination)
加減消元法係指
- 先透過乘大兩條方程,使當中某一變數前的數字變成一樣
- 再將兩條公式相加(或相減)。這樣做的結果是這條方程就只有一個變數。之後就可以利用一般嘅解方程技巧嚟計出變數的答案。
- 最後再把答案代入隨便的一條方程,咁就可以計到另一個變數的答案。
例3: 解以下聯立方程
\(\quad \quad \left\{\begin{matrix}
& 3x + 2y = 1 \quad && —— (1)\\
& x – y = -3 \quad && —— (2)
\end{matrix}\right.\)
解:
\(\begin{align}
\quad (2) \times 2,\\
\quad \quad 2x – 2y & = -6 \quad \quad —- (3)\\
(1) + (3),\\
\quad 5x & = -5 \\
x & = -1 \\
把 x = -1代入 (2) && \\
(-1) – y & = -3 \\
y & = 2 \\
\therefore \quad 方程組的解是& x = -1,y = 2。
\end{align}\)
5.1.3 圖解法 (Graphical Method)
喺坐標幾何入面,大家應學過
\(\quad \quad ax + by = c \)
其實係一條直線嚟嘅。
而對一組「聯立二元一次方程」嚟講,當中就有兩條直線。每條直線上嘅點都係符合該條直線的方程。而既然「聯立二元一次方程」嘅解係要找到同時符合兩條方程嘅值,所以從圖像上來說,兩線的相交點(Intersection)便是聯立方程的解。
例4:
解以下聯立方程
\(\quad \quad \left\{\begin{matrix}
& x – y – 2= 0 \quad && —— (1)\\
& x + y = 4 \quad && —— (2)
\end{matrix}\right.\)
解: 我地先畫出兩條直線。
- x – y – 2 = 0
| x | -2 | 0 | 2 |
| y | – 4 | -2 | 0 |
- x + y = 4
| x | 0 | 2 | 4 |
| y | 4 | 2 | 0 |
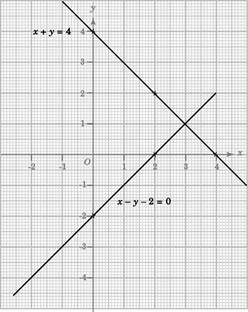
該兩條直線的交點的坐標是 (3, 1)。
從圖像可知的聯立方程的解是 x = 3及y = 1。
中二數學【目錄】
- 1. 近似與誤差 (Approximation & Errors)
- 2. 恆等式 (Identities)
- 3. 因式分解 (Factorization)
- 4. 公式 (Formulae)
- 5. 聯立二元一次方程 (Simultaneous Linear Equations)
- 6. 率及比 (Rate and Ratio)
- 7. 百份法 (Use of Percentage)
- 8. 幾何定理 (Geometry)
- 9. 畢氏定理 (Pythagoras’ Theorem)
- 10. 三角比 (Trigonometric Ratios)
- 11. 面積和體積 (Areas and Volumes)
- 12. 統計 (Statistics)
- *** 初中試卷 / 試題庫 ***
