8. 幾何定理 (Geometry)
幾何定理學D咩?
幾何學係中學數學課程入面中一個大課題。同學需要透過學習及運用不同的 幾何定理 (如「直線上的鄰角總和為180度」、「等腰三角形的底角相等」等)來解答幾何問題(一般係叫你計算某角的大小)。
喺中一嘅時候，大家其實已經接過一些較簡單的定理，詳細可以去「中一|幾何簡介」重溫。
而喺中二嘅時候，大家要學習以下幾個範疇嘅幾何定理：
- 直線上的角
- 平行線上的角
- 三角形
- 多邊形
大家要留意嘅係每一條定理都有佢嘅「簡寫」。喺學校入面老師應會要求大家做題目時寫低你用緊嘅邊條公式；但到咗日後DSE公開試，大家唔寫係無問題嘅(寫就只係攞印象分)。
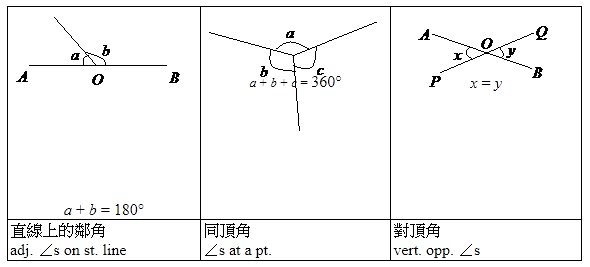
8.1 直線上的角
與直線上的角相關的定理包括：
- 直線上的鄰角 (Adjacent angles on a straight line)
意思係喺一條直線上，所有角的總和為180度。 - 同頂角 (Angles at a point)
意思係喺一個點上，所有角的總和為360度。 - 對頂角 (Vertical opposite angles)
當兩條直線相交時會有4隻角出現。兩隻對住嘅角嘅大小是相同的。
明白咗上面嘅定理解釋，日後大家要溫習，其實只要睇返下面嘅圖就可以了。
8.2 平行線上的角
當一條直線穿過一對平行線時，就會出現兩組同頂角。而所謂「與平行線上的角相關的定理」，其實係指這兩組同頂角內嘅角互相之間有咩關係。其中包括：
- 同位角 (Corresponding angles)
意思係面向同一個方位的角的大小是相同的。 - 內錯角 (Alternate angles)
意思係喺平行線內方、直線上背對(錯位)邊嘅角係相等的。- 其實大家可以利用同位角及對頂角都可以得出同一推論。
- 同旁內角 (Interior angles)
意思係喺平行線內方、直線上同一邊旁嘅角係互補的(即相加總和係180度)。- 其實大家可以利用同位角及直線上的鄰角都可以得出同一推論。
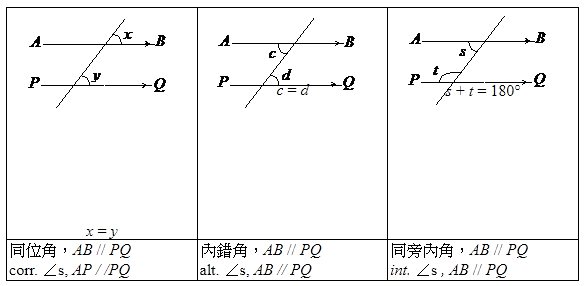
留意喺寫出定理時，大家係要寫埋邊兩條線係平行線。「//」即平行的意思。
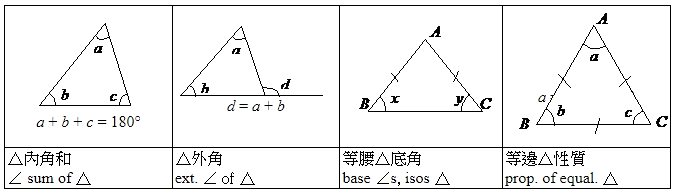
8.3 三角形
與三角形相關的定理包括：
- 三角形內角和 (Angle sum of triangle)
意思係一個三角形入面三隻角的線和為180度。 - 三角形外角
意思係把其中一條邊延長，喺外角嘅角嘅大小係另外兩隻三角形嘅內角嘅總和。 - 等腰三角形
意思係對等腰三角形來說，兩隻底角係相等的。 - 等邊三角形性質
意思係對於等邊三角形，三隻內角係相等的(即60度)
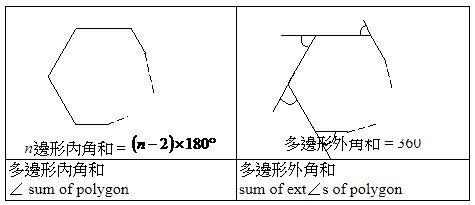
8.4 多邊形
多邊形係指由多條直線組成的一個形狀、可以係五邊形、十邊形。此外，
- 三角形其實係三邊形、長方形係四邊形。
- 如果多邊形嘅所有邊的長度相等，我地會叫個多邊做「正多邊形」。
與多邊形相關的定理包括：
- n邊形內角和 (Sum of interiod angles of n-side polygon)
n邊形內角的總和可用以下公式計出。
\(n邊形內角的總和 = (n – 2) \times 180^{\circ}\) - 多邊形外角和 (Sum of exterior angles of polygon)
這定理無寫明係”n邊形”原因係無論係幾個邊都好，所有外角嘅總和都係360度。- 但要留意所有外角嘅轉向都要一致。
