3. 因式分解 (Factorization)

3.1  因式分解的方法

3.1.1      抽公因式 (Taking Common Factor Method)

當兩個項數有相同因式嘅時，我地可以利用以往學過「抽公因數」嘅技巧，把公因式抽出嚟。

例：   因式分解 \(ab – ac\)
解： \( \quad ab – ac = a (b – c) \)

3.1.2      拼項法 (Grouping Terms Method)

所謂嘅拼項法，其實只係在因式化過程中，我地會將項數先分組，然後將各組別先因式化，之後再繼續。

例：   因式分解 ab – ac – pb + pc
解：\( \begin{array}[t]{align}
\quad ab – ac – pb + pc&= a(b – c) – p(b – c) \\
&= (b-c)(a-p)
\end{array} \)

留意當我地把前面兩項同兩面兩項抽公因式後，a(b – c) 和 p(b – c)就可以睇成係兩個項。而佢地當中都有 (b – c)，所以可以再進行抽公因式。

• 喺化簡過程中，我地只雖把 (b – c)睇成係一嚿嘢或一個待號就可以了。即可以當係化簡 az – pz咁做。

3.1.3      利用恒等式 (Using Identities)

例：  因式分解 \(4x^{2} + 12x + 9\)
解 ：\( \begin{array}[t]{align}
& 4x^{2} + 12x + 9 \\
& = (2x)^{2} + 2(2x)(3) + 3^{2} \\
& = (2x + 3)^{2} \quad \quad (利用怛等式  (a + b)^{2} = a^{2} + 2ab + b^{2})
\end{array} \)

3.1.4      十字相乘法 (Cross Method)

對於一元二多項式或方程式，若抽公因式及利用恒等式都不能將之因式分解，那便嘗試十字相乘法。

例：因式分解 \( x^{2} – x – 12\)
解：

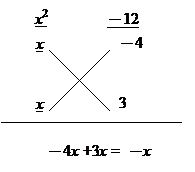\( \therefore \quad x^{2} – x – 12 = (x – 4)(x + 3) \)

數學理解力比較差嘅同學一般都唔係好明十字相乘法到底喺度做緊咩。 其實依個係一個協助我地有系統地去試嗰兩個因式出嚟嘅方法。

• 首先，題目中嘅\(x^{2}\)項嘅系數係1，所以只有 x 乘 x依個可能先會乘到一個\(x^{2}\)出嚟。
  • 當然, 2 乘 1/2 都係1，但在做因式分解嘅題目中，我地只會考慮整數。
  • 因此，因式分解後嘅兩個括號會係 (x + a) (x + b)，當中 a、b為整數(可正可負)
  • 跟住我地睇點可以乘到個常數項\(-12\)出嚟。
    • -12 = (-4) x (3)
    • -12 = (-6) x (2)
    • -12 = (-12) x (1)
    • ……
  • 當諗咗點可以乘到個常數項\(-12\)出嚟之後，我地就喺草稿紙上做「十字相相」。
    
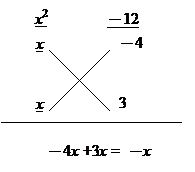
  • 而我地要睇嘅係
    • (-4) 乘 x = -4x
    • 3 乘 x = 3x
    • 加埋剛好係題目中嘅 -x，所以兩個括號就係 (x – 4)(x + 3)
    • 如果加埋唔係-x，咁我地就要試其他-12嘅組合。