8. 對稱及變換 (Symmetry and Transformation)
8.1 對稱 (Symmetry)
8.1.1 反射對稱 (Reflectional Symmetry)
- 反射對稱是指一圖形可沿一條直線分為兩個部分，其中一半是另一半的反射影像；
- 所沿的直線稱為對稱軸；
- 反射對稱圖形可以有一條或多條對稱軸（axis of symmetry）。
例1： 下面嘅圖形有兩條對稱軸。
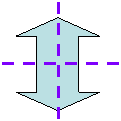
8.1.2 旋轉對稱 (Rotational Symmetry)
- 旋轉對稱是指一個平面圖形繞着某固定點旋轉一周(即360°)，而原來的圖形在旋轉過程中重複出現(即同原本嘅圖形可以完全重合)多過一次。
- 繞着旋轉的固定點稱為旋轉中心。
- 旋轉一周時如出現N個重複(包括未開始轉嗰個)，我地稱該圖嘅旋轉對稱屬N折式。
- 而每旋轉角度a時圖形重複出現，我地稱a為圖嘅旋轉角。
例2： 下面嘅圖形屬4折式、旋轉角係90°。
8.2 變換 (Transformation)
變換係指改變一個圖形的位置、方向、大小等，使它成為一個新的圖形嘅過程。
8.2.1 反射變換 (Reflection)
- 沿一條直線將圖形由直線的一邊翻轉到直線的另一邊
- 反射變換時所沿的直線稱為反射軸(axis of reflection)。
- 繪畫方法：新、舊圖各對應的點與反射的距離一樣
例3：下圖中三角形ABC沿y-軸作一反射變換就得到三角形A’B’C’。
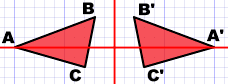
8.2.2 旋轉變換 (Rotation)
- 繞着一固定點將圖形順時針(clockwise)或逆時針(anitclockwise)旋轉。
- 固定點稱為旋轉中心(centre of rotation)。
- 繪畫方法：將原圖上每一頂點都繞旋轉中心旋轉同一角度來形成新的圖形
例4：下圖𡱒示了三角形ABC以O點為心， 順時針方向轉90°後的結果。
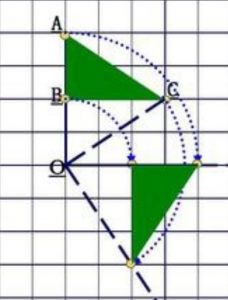
8.2.3 平移變換 (Translation)
- 把圖形沿水平和垂直的方向移動。
- 平移變換只會改變圖形的位置，而形狀、大小和方向則保持不變。
- 繪畫方法：將原圖上每一頂點按要求的方向和距離移動來形成新的圖形
例5：下圖𡱒示了三角形ABC向右移8個單位，再向上移1個單位的結果。
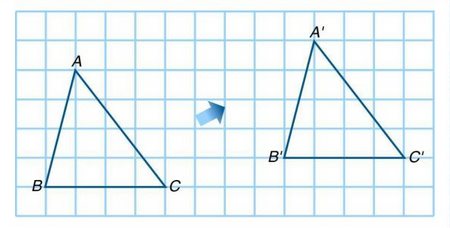
8.2.4 放大(縮小)變換 (Enlargement / Reduction)
- 將圖形的大小增加（或減少）而保持形狀不變
- 圖形的放大或縮小的倍率通常是兩個圖的邊長的比值來定義的。
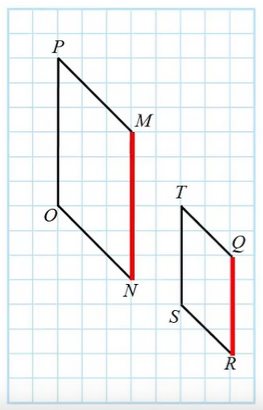
例6：在下圖中，圖形MNOP按2/3的放大率縮小至QRST。
