4. 多項式 (Polynomials)
4.1 定義
多項式是代數式的一種,由變數 (variables) 和數字經由“加、減、乘”運算組合而成的式子,並且變數中的指數必須為正整數(positive integers)及不得在根號、指數、分母等中出現。
- 以下全部都係多項式:
- \(3x + 5 \)
- \(4a – 21xy + y^{3} \)
- \(\frac{4xy^{3}}{5}\)
- 以下全部都唔係多項式:
- \(\frac{1}{x+5}\)
- \(3+\sqrt{y}\)
- 以下全部都係多項式:
4.2 詞彙
喺描述一個多項式嘅時候,經常會出現以下嘅詞彙:
- 係數:coefficient
- 常數項:constant term
- 次數:degree
- 項數:number of terms
- 遞降序:descending order
- 遞升序:ascending order
例1: 考慮多項式 \(3x^{4} – \frac{1}{2}x^{3} + 4x^{2} – x + 10\)
- 這多項式 是按變數x的降冪排列
- 項數:5
- 次數:4
- \(x^{2}\)的係數:4
- \(x\)的係數:-1
- 常數項:10
- 如按升冪排列,多項式則應寫成
\(10 – x + 4x^{2} – \frac{1}{2}x^{3} + 3x^{4}\)
4.3 多項式的加減
當要將兩個多項式相加(或相減)時,其實要做嘅嘢只係將同類項相加(或相減)。而所謂嘅同類項,係指兩個項數中嘅變數(包括指數)係樣嘅。
- 同類項相加(或相減),異項不能相加(或相減);
例:
\(\begin{align}& a + 2a + 4b \\
& = 3a + 4b\end{align}\) - 拆括號時,若括號前為+,則拆括號後每個項的符號不變;
例:
\(\begin{align}& (2a + 3xy) + (4a – xy) \\
& = 2a + 3xy + 4a – xy \\
& = 6a + 2xy
\end{align}\) - 拆括號時,若括號前為-,則拆括號後每個項的正負號要倒轉,即+變-,-變+。
例:
\(\begin{align}& (2a + 3xy) – (4a – xy) \\
& = 2a + 3xy – 4a + xy \\
& = -2a + 4xy
\end{align}\)
4.4 多項式的乘
將兩個多項式相乘嘅時候,基本上可以按以下嘅步驟先把兩個相乘嘅多項式展開:
- 先指住第一個多項式嘅第一項。
- 將被指住嘅項同後面括號括住嘅多項式入面嘅每一個項相乘。
- 乘嘅時候數字還數字乘
- 唔同嘅變數(英文字母)就同反相同嘅變數按指數定律相乘。
- 如果指住嘅唔係第一個多項式入面嘅最後一項,咁指住後面跟住嗰項,重覆第2步。
注意:如果兩個多項式分別有m個同n個項,咁展開後應有 \(m \times n\)咁多個項。 - 最後,將同類項加埋一齊。
例: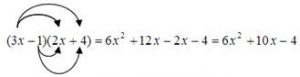
中一數學【目錄】
- 1. 有向數 (Directed Numbers)
- 2. 代數式和方程式 (Algebraic Expressions & Equations)
- 3. 指數及進制 (Laws of integral indices)
- 4. 多項式 (Polynomials)
- 5. 百分法 (Using percentages)
- 6. 近似值與估算 (Approximate values & estimation)
- 7. 幾何簡介 (Introduction to Geometry)
- 8. 對稱及變換 (Symmetry and Transformation)
- 9. 全等及相似 (Congruence and Similarity)
- 10. 量度方面的估計 (Estimation in measurements)
- 11. 面積及體積 (Area and Volume)
- 12. 坐標簡介 (Introduction to Coordinates)
- 13. 統計簡介 (Introduction to Statistics)
- *** 初中試卷 / 試題庫 ***
