3. 指數及進制 (Laws of integral indices)
3.1 指數記數法 (Index Notation)
而所謂嘅「指數記數法」其實係用嚟簡化”999個5乘埋”嘅數式。
\(\begin{align}\underbrace{5\times 5\times 5\times ….\times 5} & = 5^{999} \\
999個5乘埋 \quad \quad & \end{align}\)
一般嚟講，
\(\begin{align}\underbrace{a\times a\times a\times ….\times a} & = a^{n} & \\
n個a乘埋 \quad \quad & \end{align}\)
- 喺\(a^{n}\)入面，\(a\)稱為「底 (base)」，\(n\)稱為「指數 (index)」。
- \(a^{n}\)可以讀成 「a嘅n次方」 或 「a的n次冪」；英文讀成 n-th power of a 或 a to the power of n。
3.2 指數定律 (Laws of Indices)
指數定律基本上係指下面幾條恆等式：
\(\begin{align}
1.\quad & a^{m} \times a^{n} = a^{m + n} \\
2. \quad & a^{m} \div a^{n} = a^{m – n} \\
3. \quad & (a^{m} )^{n} = a^{m \times n} \\
4. \quad & (ab)^{n} = a^{n}b^{n} \\
5. \quad & (\frac{a}{b})^{n} = \frac{a^{n}}{b^{n}} \\
\end{align}\)
同學最緊要係識得利用上面幾條公式嚟化簡有指數嘅數式就可以了。
3.3 進制
「進制」又叫「進位制」，其實只係一種記數方式。透過進制，我地可以利用有限嘅數字或符號嚟代表所有數值。
- 可用嘅數字或符號(或元號)嘅數目稱為進制嘅基數或底數。
- 基數係 n，就叫 n 進位制。
- 嗰Ｄ數字符號就叫數碼。
大家最常用嘅當然係十進位，當中利用 10 個阿拉伯數字 0至9 嚟記數。除此之外，其實日常生活中我地都經常接觸到唔同嘅進制。例如：
- 二進制：廣泛用喺數碼設備中
- 十二進制：時辰、月份、數量單位（如一打蛋）
- 十六進制：廣泛用喺電腦程式、計數機
- 六十進制：秒、分
3.3.1 數碼 (Digits)
下面列出咗幾種進制嘅數碼同實際例子：
- 十進制 (denary system)：阿拉伯數字 0至9
e.g. 35 （因為十進制係最當用嘅，所以通常唔寫個底數10) - 二進制 (binary system)：0, 1
e.g. 11012 - 十六進制 (hexadecimal system)：0 – 9, A, B, C, D, E, F
e.g. A34F16
3.3.2 位值 (Place Value)
無論係咩進制，最右邊嘅”數碼”都係最細，代表個位。但再向左睇，每個數碼嘅值都唔同。
| 十進制 | 萬(104) | 千(103) | 百(102) | 十(10) | 個(1) |
| 二進制 | 24 | 23 | 22 | 2 | 1 |
| 十六進制 | 164 | 163 | 162 | 16 | 1 |
當我地去理解423510到底有幾大嘅時候，
- “5”係代表五個1
- “3”係代表三個10
- “2”係代表兩個100 *留意 \(100 = 10^{2}\)
- “4”係代表四個1000 *留意 \(1000 = 10^{3}\)
所以我地先叫4235做”4千升2百3十5″，亦可理解成
\(4235 = 5 + (3 \times 10^{1}) + (2 \times 10^{2}) + (4 \times 10^{3}) \)
例1： 計算出1012的值。
\(\begin{align}
101_{2} & = 1 + (0 \times 2^{1}) + (1 \times 2^{2}) \\
& = 1 + 0 + (1 \times 4) \\
& = 5
\end{align}\)
例2： 計算出AC16的值。
\(\begin{align}
AC_{16} & = 12 + (10 \times 16^{1}) \\
& = 12 + 160 \\
& = 172
\end{align}\)
3.3.3 進制間之轉換 (Conversion between numeral systems)
3.3.3.1 非十進制轉換為十進制
其實「非十進制轉換為十進制」即係講解位值入面嘅例子，比個唔係十進制嘅數你，叫你計返個值出嚟。
3.3.3.2 十進制轉換為非十進制
要將一個十進制嘅數用非十進制嘅寫法寫出嚟，我地要不斷除以目標進制基底，直到商數為 0，之後反向 取出『餘數』。
不過其實咁寫，我諗唔係好多人明。最簡單嘅方法係睇例子。
例： 把8710換為二進制
解：
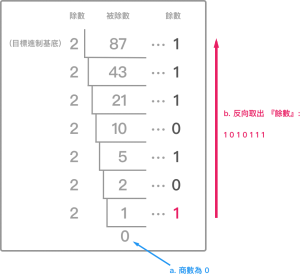
所以 8710 = 10101112
例： 把76610換為16進制
解：
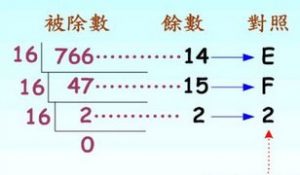
所以 76610 = 2FE16