7. 幾何簡介 (Introduction to Geometry)
幾何學(Geometry) 的拉丁文是 geometein。
- geo 是土地的意思
- metrein 是測量的意思
所以幾何學的原意係土地測量。而係數學入面,幾何學主要係研究物體形狀、大小、位置以及它們之間相互關係嘅的學科,包括點、直線、圓、曲線、平面與立體等。
7.1 重要詞彙
既然幾何學係學物體形狀,所以我地先睇一睇一D成日會提到嘅詞彙。我相信大家對當中大部份嘅詞彙都好熟識,所以喺依度只會作簡短補充。
- 點 (point)
- 頂點 (vertex)
頂點係兩條線嘅相遇點(或稱為相交點)。例如一個三角形就有3個頂點。
- 頂點 (vertex)
- 線 (line)
- 平行線 (parallel lines)
當兩條直線平行時,無論我地點將線延長,佢地永遠都唔會相交嘅。 - 垂直線 (perpendicular line)
相兩條直線係互相垂直嘅時候,佢地相交嘅地方夾住嗰隻角係90度。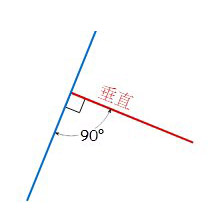
- 對角線 (diagonal line)
對角線係指一個多邊形或者多面體入面嘅兩個對角連成嘅一條線。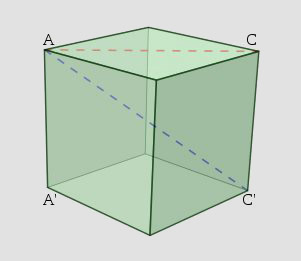
圖中AC及AC’都係對角線
- 平行線 (parallel lines)
- 角 (angle)
角係兩條線線相交嘅頂端,而嗰兩條線就叫角嘅邊。數學上,角用∠表示。而角嘅大細叫做角度。
而按角度嘅大線,角又可以細分為下面幾種:- 銳角 (acute angle)
角度大于0°且小于90° - 直角 (right angle)
角度等於90° - 鈍角 (obtuse angle)
角度大于90°且小于180° - 平角 (line angle)
角度等於180° - 反角 (reflex angle)
角度大於180°且小於360° - 補角 (supplementary angles)
相兩隻角加埋係180°嘅時候,我地會稱佢地為「互補」。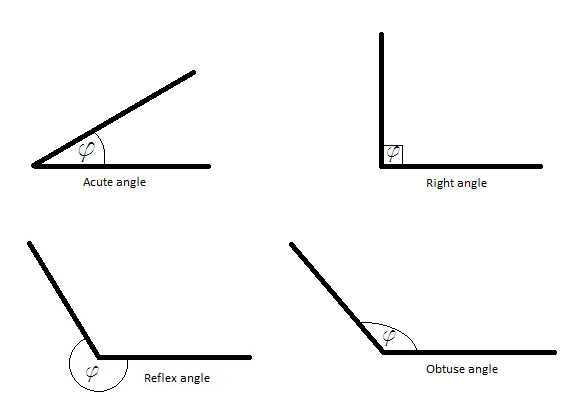
- 銳角 (acute angle)
- 平面 (plane)
簡單嚟講,一個平面可以睇成為一個平坦而擁有無窮大面積的紙。- 多邊形 (polygon)
多邊形係指由三條或以上嘅直綫圍成嘅平面圖形,也可以叫「多角形」。
係初階幾何學入面,其實我地最主要學嘅就係三角形。 - 橫切面 (cross-section)
橫切面係指與立體嘅長軸垂直嘅切面。舉個例子,一條香腸嘅橫切面就係一個圓形。
- 多邊形 (polygon)
- 三角形 (triangle)
三角形可以按「3隻角嘅大細關係」或者按「3條邊嘅長度關係」嚟分類。- 按邊長分類
- 等腰三角形 (isosceles triangle)
等腰三角形係三條邊中有兩邊係相等嘅三角形。- 兩條相等嘅邊叫腰、另一條邊叫底邊
- 兩條腰組成嘅角叫頂角、另外兩隻角叫底角。留意兩隻底角嘅角度係相等嘅。
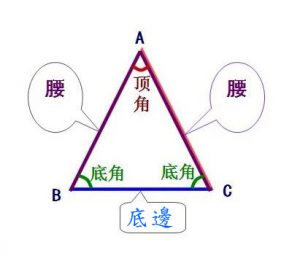
- 等邊三角形 (equilateral triangle)
等邊三角形係三邊相等嘅三角形。而3隻內角相等,都係60° - 不等邊三角形 (scalene triangle)
即係三角形入面3條邊嘅長度都唔同。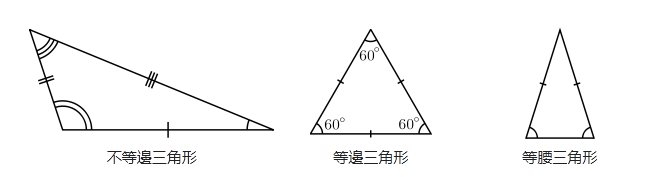
- 等腰三角形 (isosceles triangle)
- 按角度分類
- 銳角三角形 (acute-angled triangle)
銳角三角形的所有內角均為銳角(即小於90°)。 - 直角三角形 (right-angled triangle)
如果一個三角形入面有一隻角係直角(即90°),咁佢就係直角三角形。夾住直角嗰兩條邊叫直角邊,剩低嗰條(即直角對住嗰條)叫斜邊。
留意嗰兩條直角邊係可以一樣長嘅。如果係咁,個三角形就同時係等腰三角形同直角三角形,所以叫「等腰直角三角形」。 - 鈍角三角形 (obtuse-angled triangle)
當三角形入面有一隻角係鈍角(即大於90°)時,個三角形就鈍角三角形。留意一個三角形入面最多只有一個鈍角,即係其餘兩角均小於90°。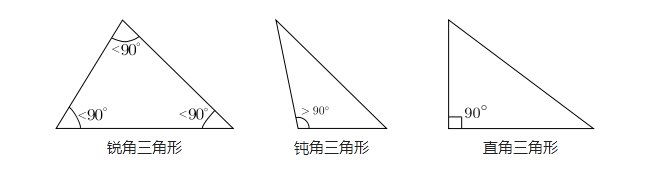
- 銳角三角形 (acute-angled triangle)
- 按邊長分類
- 立體 (3D Object)
- 圓柱體 (cylinder)
圓柱係一條由面到底嘅橫切面都係同一大細圓形嘅柱。 - 角柱體 (prism)
角柱體又名棱柱,係一條由面到底嘅橫切面都係同一大細嘅多邊形嘅柱。 - 圓錐體 (cone)
圓錐體個底係圓,但一路向上移個圓形橫切面就𧻗嚟𧻗細,去到個頂變成一點嘅立體。 - 角錐體 (pyramid)
同圓錐體差唔多,只係個底係多邊形。 - 多面體 (polyhedron)
多面體係指三維空間中由平面和直邊組成的幾何形體。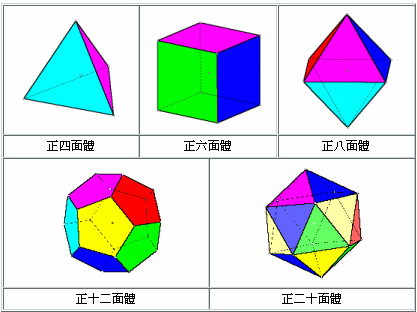
- 圓柱體 (cylinder)
7.2 定理 (Theorem)
喺依度先學同三角形有關嘅幾何定理。
直線上的鄰角 (adj. ∠s on st. line)
依個定理係指出直線上各鄰角的和係180o△內角和 (∠ sum of △)
依個定理係指出三角形嘅3隻內角嘅總和係等於180o。- 等腰△底角 (base ∠s, isos △)
依個定理係指出等腰三角形嘅兩隻底角係相等嘅。
例1:求b。
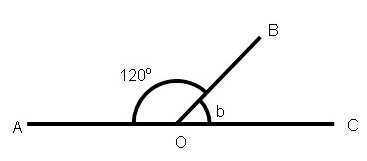
\(\begin{align} b + 120^{\circ} & = 180^{\circ} \quad \quad (直線上的鄰角) \\
b & = 60^{\circ}
\end{align} \)
留意:一般做題目嘅時候,老師都會要求同學寫低用嘅係邊條定理。如果係學英文數嘅,可以寫” (adj. ∠s on st. line)”。
例2:求∠A。
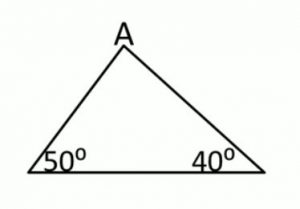
\(\begin{align} \angle A + 40^{\circ} + 50^{\circ} & = 180^{\circ} \quad \quad (△內角和) \\
\angle A & = 90^{\circ}
\end{align} \)
中一數學【目錄】
- 1. 有向數 (Directed Numbers)
- 2. 代數式和方程式 (Algebraic Expressions & Equations)
- 3. 指數及進制 (Laws of integral indices)
- 4. 多項式 (Polynomials)
- 5. 百分法 (Using percentages)
- 6. 近似值與估算 (Approximate values & estimation)
- 7. 幾何簡介 (Introduction to Geometry)
- 8. 對稱及變換 (Symmetry and Transformation)
- 9. 全等及相似 (Congruence and Similarity)
- 10. 量度方面的估計 (Estimation in measurements)
- 11. 面積及體積 (Area and Volume)
- 12. 坐標簡介 (Introduction to Coordinates)
- 13. 統計簡介 (Introduction to Statistics)
- *** 初中試卷 / 試題庫 ***
