1. 有向數 (Directed Numbers)
喺依個學習單元入面,大家要學識嘅嘢包括:
- 理解有向數的概念
- 進行有向數的四則混合運算
- 解涉及有向數的應用題
1.1 有向數的概念及相關定義
- 有向數 (Directed Number):所有附有正號(+)或負號(-)的數都稱為有向數。
例如:+9, -8, -9, +8
留意:當一個數字前面係無正負數嘅時候,個數係正嘅。 - 相反數 (Opposite Number):數值一樣但正負相反的數。
例如:+9的相反數是-9 - 絕對值 (Absolute Value):只有數值的量,不帶正或負的意義。即唔睇正負號,只睇數字嘅部份。
例如:(-9)的絕對值 = 9; (+9)的絕對值 = 9
1.2 數線 (Number Line)
依大小次序把有向數標示在一直線,該直線稱為數線。
例如:
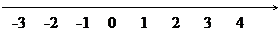
數線可以按打直定打橫嚟畫分成兩種:
- 水平數線:從左至右,由小至大;
- 垂直數線:從下至上,由小至大;
1.3 有向數的加減
數學基礎唔太好嘅同學,有時都會比有向數嘅加加減減搞到頭都大。如果你係其中一個,不如試吓學以下嘅口訣:
- 同號相加:數值相加,符號從原;
- 異號相加:數值相減,符號從大;
- 同號相減:數值相減,不夠減,符號倒轉;
- 異號相減:數值相加,符號從被減數。
例1: \( (-3) + (-8) \)
題目係兩個”同號”嘅數相加,按”同號相加”嘅口訣:
- 數值相加: 將兩個數嘅量相加。
\(8 + 3 = 11\) - 符號從原:答案嘅正負號同兩個數嘅符號一樣係”負”
- 數值相加: 將兩個數嘅量相加。
所以, \((-3) + (-8) = -11\)
例2: \( 4 + (-11) \)
題目係兩個”唔同號”(即異數)嘅數相加,按”異號相加”嘅口訣:
- 數值相減:攞兩個數嘅量相減。4唔夠減11緊要,大家當11減4咁計。
\(11 – 4 = 7\) - 符號從大:\(11\)比\(4\)大,所以答案嘅正負號係跟\(11\)嘅符號,即係”負”
- 數值相減:攞兩個數嘅量相減。4唔夠減11緊要,大家當11減4咁計。
所以, \(4 + (-11) = -7\)
例3: \( 5 – 13 \)
題目係兩個”同號”嘅正數相減,按”同號相減”嘅口訣:
- 數值相減:5細過13,唔夠減,所以我先攞13減5。
\(13 – 5 = 8\) - 不夠減,符號倒轉:因為係”5唔夠減13″,所以答案嘅符號係要倒轉。即由”正”變”負”。
- 數值相減:5細過13,唔夠減,所以我先攞13減5。
所以, \(5 – 13 = -8\)
例4: \( (-2) – 7 \)
題目係兩個”異號”嘅相減,按”異號相減”嘅口訣:
- 數值相加:攞兩個數嘅量相加。
\(2 + 7 = 9\) - 符號從被減數:被減數係”\(-2\)”,所以答案嘅符號係”負”。
- 數值相加:攞兩個數嘅量相加。
所以, \( (-2) – 7 = -9 \)
1.3.1 拆括號
拆括號其實好簡單,只要睇住括號前嘅符號係正定負,按法則咁做就得:
- 如括號前面係”正”,我地只需要當個括號無到就可以了。
例:
\( \begin{align} 3 + (6 – 8) &= 3 + 6 – 8 \\
&= 9 – 8 \\
& = 1
\end{align}\) - 如括號前面係”負”,我地把括號攞走嘅時候,入面每一個數嘅符號都要倒轉。
例:
\( \begin{align} 3 – (6 – 8) &= 3 – 6 + 8 \\
&= 11 – 6 \\
& = 5
\end{align}\)
當然依條數可以用下面兩個方法嚟計:- 先計括號入面嘅數,再拆括號嚟計
\( \begin{align} 3 – (6 – 8) &= 3 – (-2) \\
&= 3 + 2 \\
& = 5
\end{align}\) - 先計括號入面嘅數,之後用”異號相減”口訣:
\( \begin{align} 3 – (6 – 8) &= 3 – (-2) \\
& = 5
\end{align}\)
- 先計括號入面嘅數,再拆括號嚟計
其實拆括號好多時只係想化簡四則運算,例如
- \(3 – (-2)\)可以透過拆括號變成\(3 + 2\)
- \(4 + (-3)\)可以透過拆括號變成\(4 – 3\)
如同學對有向數嘅概念掌握得好,唔拆括號直接計都得。
1.4 有向數的乘除
有向數嘅乘除嘅口訣好易記,相信好多老師都會教大家。
- 正正得正;負負得正;
- 正負得負;負正得負。
例1: \( (-2) \times 7 \)
題目係兩個”負正”嘅相乘,所以答案係一個負數。而答案嘅量係 \(2 \times 7 = 14\)。
所以 \( (-2) \times 7 = -14\)
中一數學【目錄】
- 1. 有向數 (Directed Numbers)
- 2. 代數式和方程式 (Algebraic Expressions & Equations)
- 3. 指數及進制 (Laws of integral indices)
- 4. 多項式 (Polynomials)
- 5. 百分法 (Using percentages)
- 6. 近似值與估算 (Approximate values & estimation)
- 7. 幾何簡介 (Introduction to Geometry)
- 8. 對稱及變換 (Symmetry and Transformation)
- 9. 全等及相似 (Congruence and Similarity)
- 10. 量度方面的估計 (Estimation in measurements)
- 11. 面積及體積 (Area and Volume)
- 12. 坐標簡介 (Introduction to Coordinates)
- 13. 統計簡介 (Introduction to Statistics)
- *** 初中試卷 / 試題庫 ***
