9. 全等及相似 (Congruence and Similarity)
9.1 基礎概念
- 全等
- 指兩個圖形的形狀和大小都完全相同。
- 一個圖經平移、反射或旋轉變換後,可得一個與原來全等的圖形。
- 相似
- 指兩個圖形的形狀相同。
- 一個圖形經放大或縮小變換後,可產生一個與原來相似的圖形。
兩個全等圖形必同時也是相似圖形。
9.2 全等三角形 (Congruent Triangles)
- 當兩個三角形全等時,它們所有對應邊 (corresponding sides) 和所有對應角 (corresponding angles) 都相等。
- 「三角形ABC全等於三角形XYZ」可寫成為 \(\triangle ABC \cong \triangle XYZ\)
- 當中的「\(\cong\)」代表全等。
- 須依照對應角之位置寫出△。
9.2.1 三角形全等的條件
試想像老師向每位學生派3支長度分別係3cm、4cm、5cm的木條,然後叫大家砌出一個三角形。請問有同學能砌出一個與其他人不同的三角形嗎?
無錯!係無可能嘅。所有人砌出嚟嘅三角形都係一樣嘅。所以,只要「兩個三角形三對嘅對應邊都相等」,咁依兩個三角形就係全等(即一模一樣)。為方便書寫,
- 有一對對應邊(side)相等,會寫一個S (S = Side)
- 有一隻對應角(angle)相等,會寫一個A
所以,「三對嘅對應邊都相等」會記作「SSS」。
當明白咗S、A代表咩之後,我地可以重溫一吓能證明返兩個三角形全等嘅條件:
- SSS
3對對應邊相等。 - SAS
兩對對應邊相等、而且夾住嗰對應角都相等。 - ASA
兩對對應角相等、而兩隻角之間嘅邊都相等。 - AAS
其實因為「三角形內角和係180度」,所以當有兩對對應角係相等嘅時候,第3對對應角都係會相等嘅。因此,當AAS出現嘅時候,其實即係ASA出現,可以唔去記7 (所以喺下面總結嘅圖入面,AAS係灰咗嘅)。 - RHS
- R 代表兩個三角形都有隻直角 (right angle)
- H 代表斜邊 (hypotenuse)相等
- S 代表有對對應邊相等
下面嘅圖就係總結咗喺唔同嘅條件下,嗰兩個△係會點「全等」。大家大可試吓可唔可以按住條件咁畫,而又畫到一個唔同嘅△出嚟。 (畫到嘅話我諗可以去攞諾貝爾法斯特奬!)
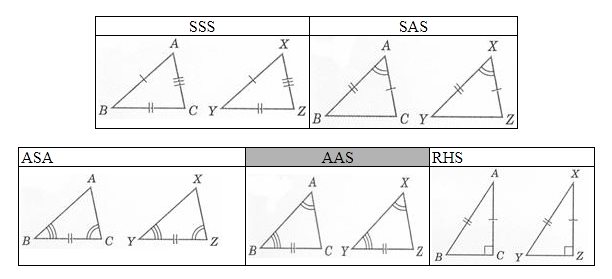
再提一提大家:
- 在上圖中,\(\triangle ABC \cong \triangle XYZ\) 不可寫作 \(\triangle ABC \cong \triangle YZX\)。咁係因為我地一定要依照對應角之位置寫出△。
注意: SSA不能用作證明全等三角形。
下圖中嘅 △DAB 同 △DAC,
- DA = DA (公同邊)
- AB = AC (因為AB同AC都係以A點畫嘅圓嘅半徑)
- \(\angle BDA = \angle CDA\)
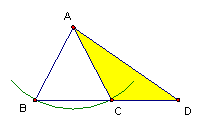 因此條件「SSA」出現咗,但好明顯△DAB 同 △DAC係唔一樣嘅。
因此條件「SSA」出現咗,但好明顯△DAB 同 △DAC係唔一樣嘅。
9.3 相似三角形 (Similar Triangles)
- 若兩個三角形相似,即代表
- 佢地嘅對應角相等。
- 佢地嘅對應邊成比例 (corresponding sides are proportional),即3對對應邊嘅邊長比例係一樣嘅。
- 「三角形ABC和三角形XYZ相似」可寫成為 \(\triangle ABC \sim \triangle XYZ\)
- 當中的「\sim」代表相似。
- 須依照對應角之位置寫出△。
9.3.1 三角形相似的條件
可以證明兩個三角形係相似嘅條件包插:
- AAA~
當3對對應角相等嘅時候,兩個三角形嘅形狀會一樣,所以係相似嘅。 - SSS~
留意唔係”SSS”,係多咗個”~” (相似符號的)。依度「SSS~」係代表3對對應邊嘅比例相等。因此兩個三角形嘅狀會一樣(即係相似)。 - SAS~
依個同SSS~差唔多,主要都係因為有一對對應角相等,所以當旁邊嘅對應邊比例相等時,兩個三角形嘅形狀都係會一樣。
面嘅圖就係總結咗喺唔同嘅條件下,嗰兩個△係會點「相似」嘅。
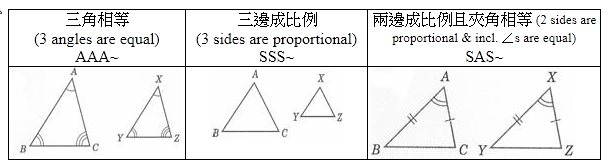
9.3.2 相似三角形特性
如\(\triangle ABC \sim \triangle XYZ\),則
- 對應角相等。即
∠A = ∠X; ∠B = ∠Y; ∠C = ∠Z - 3對對應邊嘅比例都係一。即
\(\frac{AB}{XY} = \frac{BC}{YZ} = \frac{CA}{ZX} \)
中一數學【目錄】
- 1. 有向數 (Directed Numbers)
- 2. 代數式和方程式 (Algebraic Expressions & Equations)
- 3. 指數及進制 (Laws of integral indices)
- 4. 多項式 (Polynomials)
- 5. 百分法 (Using percentages)
- 6. 近似值與估算 (Approximate values & estimation)
- 7. 幾何簡介 (Introduction to Geometry)
- 8. 對稱及變換 (Symmetry and Transformation)
- 9. 全等及相似 (Congruence and Similarity)
- 10. 量度方面的估計 (Estimation in measurements)
- 11. 面積及體積 (Area and Volume)
- 12. 坐標簡介 (Introduction to Coordinates)
- 13. 統計簡介 (Introduction to Statistics)
- *** 初中試卷 / 試題庫 ***
