集合的記法
16.1 認識 集合 的記法,包括併集、交集和餘集的記法 (Recognizing the Notation of Set Language including Union, Intersection and Complement)
集合 喺最近嘅會考課程入面係冇嘅,不過喺舊D嘅會考課程入面就有。
而根據HKDSE課程嘅要求,大家只需認識D記法。
- 其實咁都有好處,就係大家只要明咗D記法,咁講概率嘅時候會更易講。
簡單嚟講,集合就係“一堆嘢喺埋一齊”。而集合入面嘅嘢就係“元素”。
- 例如“由1至10嘅雙數”集合就係包括有“2, 4, 6, 8, 10”五個元素。
- 而用集合嘅記法就係: 由1至10嘅雙數 = { 2, 4, 6, 8, 10 }
- “{ }”就係代表咗集合,而入面嘅每一樣嘢就係一個元素。
- 而通常我哋亦會用大寫英文字母嚟代表一個集合。
- 例如設 A 為由1至10嘅雙數嘅集合,咁
A = { 2, 4, 6, 8, 10 }
- 例如設 A 為由1至10嘅雙數嘅集合,咁
- 留意集合並唔單止係用喺“數字”上,用喺其他物件上都得。例如:
- 有31號嘅月份 = { 1月, 3月, 5月, 7月, 8月, 10月, 12月}
- 首5個英文大寫字母 = { A, B, C, D, E }
除咗記法之外,我哋亦要學幾個“集合嘅運算”,包括“併”、“交”同埋“餘”。
16.1.1 併集 (Union)
“併 (Union)”簡單嚟講即係“將兩個集合加埋”。
- 併嘅符號係 ∪(好似英文U字)。
而“併集”就係即兩個集合加埋後嘅嗰個集合(即係結果)。亦有人叫併集做“聯集”。
A∪B = {1, 2, 3, 4, 6}
C∪D = {1, 2, 3, 4}
16.1.2 交集 (Intersection)
“交”簡單嚟講係“將兩個集合重叠取交义嘅部份”(亦可以話取相同嘅部份)。
- 交嘅符號係 ∩(好似倒轉嘅英文U字)。
而“交集”就係即兩個集合相“交”後得出嘅集合。
C ∩ D = {3}
A ∩ B = ∅
§ “∅”係”空集合” (個符號好似O打斜畫多一畫),代表一個冇嘢嘅集合。
16.1.3 餘集 (Complement)
“餘”簡單嚟講即係“搵一個集合攞剩嘅部份”。
至於要明白咩係“攞剩”,我哋先要學咩係“全集”。
- “全集”即係包括晒所有元素嘅集合。
- 而對唔同話題嚟講,“實際”嘅全集係會唔同嘅。
- 例如:
月份嘅全集 = {Jan, Feb, Mar, Apr, May, Jun, Jul, Aug, Sep, Oct, Nov, Dec}
彩虹顏色嘅全集 = { 紅, 橙, 黃, 綠, 青, 藍, 紫 }
- 例如:
- 前返前面嘅例子:“有31號嘅月份”集合 = { 1月, 3月, 5月, 7月, 8月, 10月, 12月}
- 咁“有31號嘅月份”集合嘅“餘集”= { 2月, 4月, 6月, 9月, 11月 }
- 符號方面,如果一個集合係用A嚟代表(你可以當A只係個“變數”)。咁A嘅餘集就係 \(\bar{A}\) (即係喺A上面加一畫)。
- 有時我哋亦會叫餘集做“補集”(好似有個“補返落去就完整”嘅意思)。
1.6.4 集合嘅圖表法 – 溫氐圖(Venn Diagram)
當大家大約知道咩係集合嘅時候,又係講數學家點“偷懶”嘅時候。
- 為咗唔駛成日列晒D元素出嚟,數學家就諗咗用“溫氏圖”嚟表示集合嘅概念。
喺溫氏圖入面,
- 全集係用一個長方形嚟代表(長方形內空間就係“全世界”)。
- 集合通常會用一個個圓形代表,而圓形上會標明集合該集合嘅“字母”。
- 圓形內嘅部份就代表集合嘅元素(好以包住咗D元素咁)。
而如果用溫氏圖,A ∪ B就可以用下圖嚟表達:
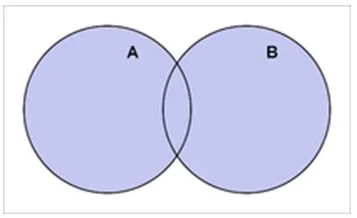
- 圖中兩個圓形重叠部份係代表A、B兩個集合有相同嘅元素。
- 如果A、B兩個集合冇相同元素,咁兩個圓形就會分開。
- 點都好,A、B嘅“併集”係最終有顏色嘅“部份”
而A ∩ B就可以用右面幅圖嚟表達:
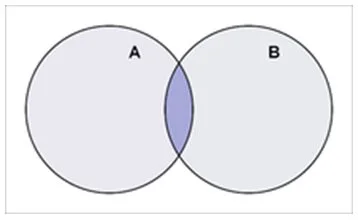
- A、B嘅“交集”就係兩個圓形嘅“重叠部份”。
- 而如果兩個圓形冇重叠,咁咪即係代表“交集”係“冇嘢”,即 A ∩ B = ∅
而於用圖嚟表達“餘集”嘅概念,
- 因為長方形係代表“全集”,所以“A嘅餘集”就係“圓形A外面嘅部份”。
講到依到,希望大家覺得用圖嚟代表集合都好易明。但其實“集合”係一個好深奧嘅課題。
- 只不過喺中學文憑講集合只係為咗方便深D嘅概率概念。
- 所以大家只要有個idea就OK,仲有記住符號 ∪、∩ 同溫氐圖嘅概念。
