13. 三角比 > 三角函數的定義

13.1.   三角函數的定義

三角比函數的定義 係由直角三角形度發展出嚟嘅。要學好 三角比函數 ，最基本條件係要能夠清楚咁講出一個直角三角形入面嘅資料。

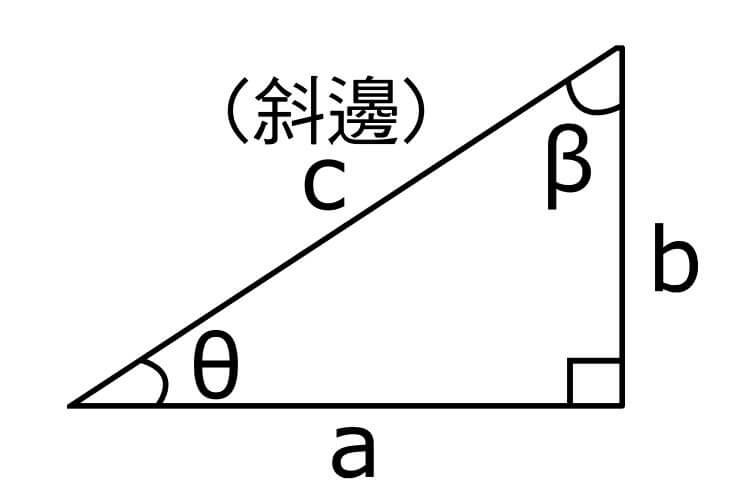喺右圖中的直角三角形入面，

• 有三條邊，邊長分別為 a, b, c
• 另三隻角當中有一隻係直角
• “斜邊”永遠係直角對面嘅邊
• 另外兩條邊可以叫作“鄰邊”及“對邊”。但邊條係“對邊”就要睇你攞住邊隻角嚟講。
  • 對 \(\theta\) 嚟講
    • a 係“鄰邊” (即 \(\theta\) 旁邊嘅邊)
    • b 係“對邊” (即 \(\theta\) 對面嘅邊)
  • 對 \(\beta\) 嚟講
    • b 係“鄰邊” (即 \(\beta\) 旁邊嘅邊)
    • a 係“對邊” (即 \(\beta\) 對面嘅邊)

三個基本嘅三角比函數 (sin, cos, tan) 嘅定義係:

• \(\sin \theta = \dfrac{對邊}{斜邊} \)
• \(\cos \theta = \dfrac{鄰邊}{斜邊} \)
• \(\tan \theta = \dfrac{對邊}{鄰邊} \)

好多教科書會寫 \(sin \theta = \dfrac{a}{c} ，cos \theta = \dfrac{b}{c} ，tan \theta = \dfrac{a}{b} \)。但大家一定要留意當中嘅 a、b、c 一定係 \(\theta\) 嘅對邊、對邊及斜邊。 所以大家都係記 \(\sin \theta = \dfrac{對邊}{斜邊} \) 等嘅公式吧。