13. 三角比 > 三角函數基本運用

13.2. 三角函數基本運用

每一個三角函數嘅定義都有兩條邊一隻，所以 三角函數基本運用 就係比其中兩個你，然後要係計返剩低嗰個(可能係邊或角)。

而當中最緊要嘅係

• • 記得sin, cos, tan 嘅定義
  • 然後擇個啱用嘅定義嚟計條數

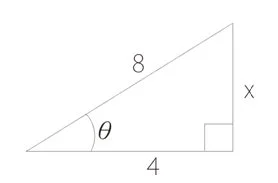例1：        求右圖中的未知數 x 及 θ。
解說：    大家首先養成一個「見到直角三角形要計未知數能先睇嘅用唔用到三角函數」嘅習慣。

• 因為題目比咗直角三角形中嘅兩條邊，所以利用三個函數，其他嘅邊同角都一定可以計到。
• 計算 θ 的思路
  • 我哋應先判斷對θ 嚟講，條”4嘅邊”同”8嘅邊”係咩邊(即鄰邊、斜邊定對邊)
    • 4是 θ 的鄰邊
    • 8 係直角對面嘅邊，所以佢係斜邊
  • 包含鄰邊同斜邊的三角函數是 cos
  • 所以我哋要嘅式係： \( cos \theta = \dfrac{鄰邊}{斜邊} \}
  • 即 \( cos \theta = \dfrac{4}{8} \)
            \(\theta = 60^{\circ} \)
• 計算 x 的思路 (一)
  
  • 因x是一條邊，所以如果用三角函數，我哋要知道另一條邊同一隻角
    • 已知 θ = 60^o；
    • 另一條邊可選 “4”
  • 因為我哋用θ，所以x是“對邊”，“4”係“鄰邊”
  • 包含對邊及鄰邊的三角函數係 tan
  • 所以我哋要嘅式係： \( tan \theta = \dfrac{對邊}{鄰邊} \}
  • 即 \( tan 60^{\circ} = \dfrac{x}{4} \)
            \( x = 4 \times tan 60^{\circ} = 6.93 \)
• 計算 x 的思路 (二)
  • 同思路(一)差唔多，只係我地係嘅唔係”4邊”而係”8邊”
    • 8邊係”斜邊”
  • 包含對邊及斜邊的三角函數係 sin
  • 所以我哋要嘅式係： \( sin \theta = \dfrac{對邊}{斜邊} \}
  • 即 \( sin 60^{\circ} = \dfrac{x}{8} \)
            \( x = 8 \times sin 60^{\circ} = 6.93 \)
• 計算 x 的思路 (三)
  • 除咗用三角比函數，我地都可以用畢氏定理。