1. 解方程 > 解一元一次方程

Level 1.0

\(\quad 3x = 6 \)

我諗所有同學都知道　“x等於 6 除 3”。即  \( \quad   x = \dfrac{6}{3} = 2 \)

Level cleared!

Level 1.1

\(\quad 2x = \dfrac{7}{3} \)

其實這條目跟“3x = 6”係一樣嘅，只係數字變咗。由“3x 等於 6”變成“2x 等於 2份之7”。 所以

\(\quad x = \dfrac{7}{3} \div 2 = \dfrac{7}{3} \times \dfrac{1}{2}  = \dfrac{7}{6} \)

請同學確保自己識得點用計數機計到以上答案！

Level cleared!

Level 1.2

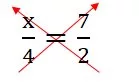
\(\quad \dfrac{x}{4} = \dfrac{7}{2}\)

其實依條題目同“ \(2x = \dfrac{7}{3} \)”又係一樣，只係“\(2x\)”變咗做“\(\dfrac{x}{4}\) ”。喺度同學可以用“交义相乘”嚟化簡條數式！！

“交义相乘”嘅方法係好似右圖咁樣嘅。     

“交叉相乘”後條數式變成   \( 2x = 28\)。 一睇又係一條 level 1.0嘅題目。

當然，同學大可就咁把左邊分母的4搬去右邊，變成
\( x = \dfrac{7}{2} \times 4 = 14\)。喺依度，我嘅重點係令大家知道其實計嚟計去,D解方程都係可以一步步咁去解。

Level cleared!

Level 2.0

\(\quad 4x + 6 = 9 \)

喺度，我哋須要用移項嘅方法將“同類項”放埋同一邊，即係：
\(\quad 4x = 9 {\color{Red} – 6 } \)

溫習：當我哋移“加減”嘅項數去“＝”嘅另一邊時，我哋要“加變減、減變加”。 下一步計埋“\(9 – 6\)”，就得到
\(\quad 4x = 3 \)

又係一條level 1.0嘅題目！！ 答案： \(x = \dfrac{3}{4}\)

Level cleared!

Level 2.1

\(\quad 4x – 5 = 8x + 7\)

喺度，我哋一樣要先用移項嘅方法將同類項放埋一齊（即x喺一邊，數字喺另一邊），
\(\quad 4x – 8x = 7 + 5\)

留意　“－5移去另一邊變成＋5”，“8x移去另一邊變成－8x”。

繼續計埋條數：
\(\quad -4x = 12\)
馬上變成一條level 1嘅題目！
\(\quad x = \dfrac{12}{-4} = -3\)

Level cleared!

Level 3.0

\(\quad \dfrac{1}{2}x + 5 = 3x + \dfrac{1}{4}\)

同學可以用level2嘅技巧做依條數，做法如下：

\(\begin{align}
\dfrac{1}{2}x + 5 & = 3x + \dfrac{1}{4} \\
\dfrac{1}{2}x – 3x & = \dfrac{1}{4} -5 \\
-2.5x & = -47.5 \quad \quad (我係用計算機計\dfrac{1}{4} – 5嘅) \\
x & = 1.9 \quad \quad \quad (又係用計算機計嘅!!)
\end{align}\)

當我地見到份數時，其實同學亦可以用“全條式乘一個數字”嘅方法嚟先將題目簡化。

用返上面嘅例子：題目中的份母有2及4，所以我們乘4。即

\(\begin{align}
4 \times \left ( \dfrac{1}{2}x + 5 \right ) & = 4 \times \left ( 3x + \dfrac{1}{4} \right ) \\
4 \times \dfrac{1}{2}x + 4 \times 5 & = 4 \times 3x + 4 \times \dfrac{1}{4} \\
2x + 20 & = 12x + 1 \\
\end{align}\)

咁就又變成一條level 2嘅題目! 相信大家都應識點應付level 2嘅題目了。

留意喺拆括號嘅時候，每一項都要乘４。
好多同學有時會犯以下嘅錯：

\(\begin{align}
4 \times \left ( \dfrac{1}{2}x + 5 \right ) & = 4 \times \left ( 3x + \dfrac{1}{4} \right ) \\
4 \times \dfrac{1}{2}x +{\color{Red} 5 } & = 4 \times 3x + {\color{Red} \dfrac{1}{4} }
\end{align}\)

** 上面紅色的部份喺拆括號時冇乘４，所以錯!!

Level cleared!

Level 3.1

\( \dfrac{1}{6}x + 5 = \dfrac{2}{9}x + 1\)

見到份母有6同9，咁我哋到底要乘咩數字呢？

• 有人話要乘6同9嘅最小公倍數(LCM，即18)。
  你計到當然好。但如果分母係有27, 39呢?
• 其實我哋可以咩都唔理，照乘6同9（即係乘“54”）。反正都係交比計數機去計。

數字係大咗，不過反正我哋有計算機可以用，咁計 \(5 \times 18\) 同 \(5 \times 6 \times 9\) 又有咩分別呢？！

全條式乘“6×9”，即每一個數乘“\(6 \times 9\)”:

\(({\color{Red}6} \times 9) \times\dfrac{1}{6}x + (6 \times 9) \times 5
= (6 \times {\color{Red}9}) \times\dfrac{2}{9}x + (6 \times 9) \times 1 \)

留意紅色嘅份母係有得約數嘅，所以：

\(\begin{align}
9x + 270 & = 12x + 54 \\
9x – 12x & = 54 – 270 \\
-3x & = -216 \\
x & = 72
\end{align}\)

熟咗依個方法之後可以做快一點！

例： \(\quad \dfrac{2}{5}x + 5 = \dfrac{2}{9}x + 3\)
解：

\(\begin{align}
\dfrac{2}{5}x + 5 & = \dfrac{2}{9}x + 3 \\
18x + 225 & = 10x + 135 \quad \quad (左右乘 5 \times 9) \\
18x – 10x & = 135 – 225 \\
8x & = –90 \\
x & = -11.25
\end{align}\)

Level cleared!

\(\dfrac{5}{x + 4} = \dfrac{4}{2x – 3} \)

數學唔好嘅同學可能會覺得條數有D怪。但其實同學只要睇到依條係“一元一次方程”，再留意到條數嘅樣好似“交义相乘”嘅“\(\dfrac{A}{B} = \dfrac{C}{D}”形式，就應該可以好似下面咁開始計條數：

\(  5 ( 2x – 3 ) = 4 (x + 4)       \\
…… 拆括號後又變咗做level 2 題目！！
\)

Level cleared!