14. 平面及立體圖形 > 扇形的面積及弧長

14.3.   扇形的面積及弧長 (Area of a Sector & Length of an Arc)

扇形 只係“圓形嘅一部份”，也可以理解為喺圓形蛋糕度切一件出嚟嘅形狀。

右圓顯示咗一個圓形及扇形。留意：

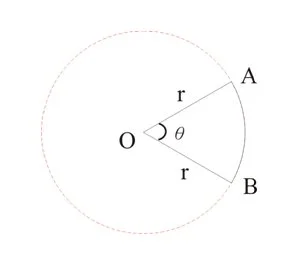
• 紅色虛線係一個圓形
  • 其半徑為r
• 黑線部份就係一個扇形
  • 可記作 扇形AOB
  • 曲線AB稱為“弧長AB”，記號係  \({\stackrel{\Large\frown}{AB}}\)
• 如果把A、B兩點用直線連起，扇形將會被分成兩部份：
  • 左邊嘅係一個三角形
  • 右邊嘅係一個“弓形”

14.3.1 扇形面積

一個圓形嘅圓心角係\(360^{\circ})。假設扇形嘅角度係θ。按比例，

\(扇形面積 = 圓形面積 \times \dfrac{\theta}{360^{\circ}} \)

即，  \(扇形面積 = \pi r^{2} \times \dfrac{\theta}{360^{\circ}} \)

14.3.1 弧長

同一個定理，按圓形周界同弧長嘅比例

\(弧長 = 2\pi r \times \dfrac{\theta}{360^{\circ}} \) 　

14.3.2 扇形周界及弓形面積

扇形周界同弓形面積係冇公式的。下面嘅算式只係提大家點計佢地出嚟。

• 扇形周界 = 弧長 + 2個半徑
• 弓形面積 = 扇形面積 － ΔOAB面積
  （ΔOAB面積 =  \(\dfrac{1}{2}absin\theta\)  計，其中a = b = r）