14. 平面及立體圖形 > 立體圖形的表面積及體積

球體嘅題目一般都平較容易，較少出D好“陰濕”嘅數。

至於要留意嘅地方包括：

• 留意題目俾你嘅係“半徑”定“直徑”
  （公式入面嘅“r”係半徑）
• 留意係計緊半個波定一個波
  • 如果計半個波嘅體積，只要將條式 “\(\times \dfrac{1}{2}\)” 就得。
  • 如果題目要求計半個波嘅“總表面面積”，留意除咗個波嘅表面曲面積 “\(4\pi r^{2} \times \dfrac{1}{2} \)”之外，仲要加個底圓嘅面積（即\(\pi r^{2}\))。即
    半球體線表面面積 = \(4\pi r^{2} \times \dfrac{1}{2} + \pi r^{2} \)

柱體

• 名符其實係“一碌柱”，即底部同頂部嘅橫切面係一樣嘅。
• 個底（或者面）嘅形狀就決定咗個柱體叫咩名。
  例如下圖度就有一個長方柱體和圓柱體(為方便明白，個底填咗做黃色)。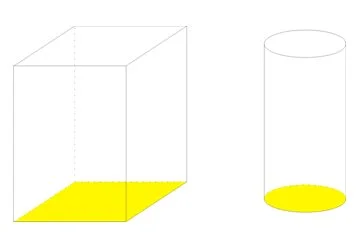
  
• 只要柱體嘅底唔係圓形而係“起角”，我哋可以統稱似一類嘅體做“角柱體”。

如何計算柱體體積？

• 所有柱體嘅體積都係 “底面積 x 高”
  

如何計算柱體總表面面積？

• 一般題目指嘅總表面面積係包括下列幾個面嘅面積線和
  • 面
  • 底
  • 包住柱身嘅所有側面
    例如喺長方柱體度，就有四個側面。
• 但實際計數時要小心一點。
  • 因為有時題目要你計嘅“總表面積”係唔包括個“面”嘅。
  • 例如題目係 “有一個圓柱體水杯，半徑3cm。如水高5cm，求被水弄濕的總表面面積” 嘅時候，因為水只接觸到底同四周，所以
     被水弄濕的總表面面積 = 底圓面積 + 側面高5cm嘅面積”。
• 計“側面面積”時，一個快D嘅方法係想像將個柱體嘅側面剪開。例如下面嘅三角柱體就有三個側面。如果將柱體打開，三個側面就會形成一個長方形。
  
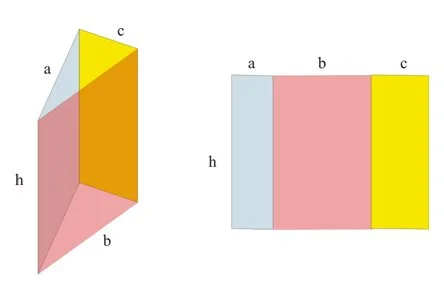
  \(\begin{align}
  \therefore & 長方形側面面積 \\
  & = 柱體打開後長方形面積 \\
  & ＝ 柱底圖形嘅周界 \times 柱嘅高度
  \end{align}\)
• 根據以上一點：
  \(\begin{align}
  \therefore & 圓柱側面面積 \\
  & ＝ 底圓周界 \times 柱嘅高度 \\
  & = 2 \pi rh
  \end{align}\)

錐體

• 錐係用來鑽孔的尖銳器具。
  所以錐體個底係一個面而個頂係一點嘅立體圖形。
•  如果個底係圓形嘅就叫“圓錐體”，個底係三角形就叫“三角錐體”。
• 至於“正錐體”（如正三角錐體）就係指個頂點喺係個底嘅正中心度（通常會考題目考嘅錐體都係正錐體）。

如何計算錐體體積？

• 錐體嘅體積 = \(\dfrac{1}{3} \ times 底面積 \times 高\)
  • 例如 \(圓柱錐體積 = \dfrac{1}{3}\pi r^{2} h \)

如何計算錐體總表面面積？

• 因為錐體嘅頂只係得一點，所以沒有“頂部的面積”。因此：
  　總表面面積 = 底面積 ＋ 四圍嘅側面面積
• 計角錐體側面面積嘅方法如下：
  • 圓錐體嘅側面面積係有公式嘅
    \(圓錐體側面面積 = \pi r l \)
    當中  r = 底圓嘅半徑； l = 圓錐體嘅斜邊邊長
  •  至於其他錐體嘅側面面積就要一個個咁利用三角形面積嘅公式去計。