12. 演繹推理幾何 > 相似三角形

12.5.  相似三角形 (Similar Triangles)

講 相似三角形 ，首先當然要講吓個定義…

• 相似 
  • 指兩個圖形嘅形狀相同。
  • 一個圖形經放大或縮小變換後，可產生一個與原來圖形相似嘅圖形。

相似 嘅符號係 \(\sim\)

• \(\triangle ABC 與 \triangle XYZ 相似 可寫成 \triangle ABC \sim \triangle XYZ \)
  （留意一定要跟對應角嘅位置寫出△的名字）

12.5.1 相似三角形性質

當兩個△係相似時，如 \(\triangle ABC \sim \triangle XYZ \)

• 佢哋嘅對應角相等
   \(\angle A =\angle X， \angle B = \angle Y，\angle C = \angle Z \)
• 佢哋嘅對應邊嘅比例相等 (corresponding sides are proportional)
  \(\dfrac{AB}{XY} = \dfrac{BC}{YZ} = \dfrac{CA}{ZX} \)

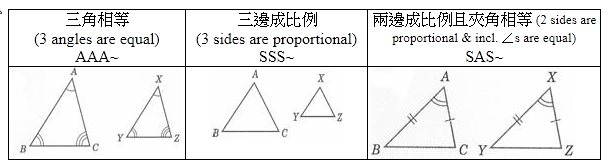
12.5.2  相似三角形的條件

明白咗上面嘅基本嘢之後，更加緊要嘅係知道幾時兩個三角形先係相似。下面幅圖已總結咗相似嘅條件：

12.5.3.  公開試提點

• 相似三角形 考得多過 全等三角形。
  • 依個係因為相似相似三角形嘅題目可以連埋“相似圖形的面積及體積”嚟考。即要求你睇到邊兩個△相似，然後利用“相似△特性”中嘅邊長比嚟求其他邊或計兩個圖形嘅面積比。
• 全等同相似三角形好多時都係考“證明題”（例如叫你證明 \(\triangle ABC \sim \triangle XYZ \)）。
  • 同學一般都覺得依D題目比較難。
  • 基於題目叫你得證明嘅嘢係一定啱，要做嘅嘢係寫出點解我哋知道佢係啱就得。

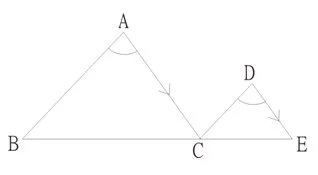例1：在右圖中，∠BAC =∠CDE；證明\(\triangle ABC \sim \triangle DCE \)
解說：

• 先要諗吓有咩方法可以證明兩個△相似，再睇吓可以用邊個方法。
• 因為題目冇提過邊長，所以可以用嘅只有 “三角相等”。
  • 因此我哋要寫低點解三隻角相等

寫法如下：

\(\begin{align}
\angle BAC & = \angle CDE  （已知）\quad \quad {\color{Red} \leftarrow } 依行講點知道第一隻角相等 \\
\angle ACB & = \angle DEC  （同位角，AC//DE）\quad \quad {\color{Red} \leftarrow }依行講點知第二隻角相等 \\
\angle ABC & = \angle DCE （△內角和）\quad \quad {\color{Red} \leftarrow }因兩個△已有兩隻角相等，所以第三隻角都會相等 \\
\therefore \quad   △ABC & \sim △DCE  （三角相等） \quad \quad {\color{Red} \leftarrow }因三隻角相等，所以可以寫出佢哋係相似嘅 \\
\end{align}\)