12. 演繹推理幾何 > 畢氏定理

12.6. 畢氏定理 (Pythagorean Theorem)

畢氏定理指出，喺一個直角三角形(Right-angled triangle)入面

• 兩條直角邊的長度的平方和等於斜邊長度的平方

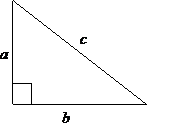
\(即 \quad \quad a^{2} + b^{2} = c^{2} \)

注意：直角△最長嗰條邊叫“斜邊”(hypotenuse)，即公式中嘅 c。

12.6.1.  畢氏定理的主要用途

畢氏定理嘅題目主要係考：

• 比一個直角三角形你，利用已知的其中兩條邊嘅長度，運用畢氏定理嘅公式計算出第三條邊嘅長度。
• 當知邉晒三角形入面嘅三條邊長度之後，利用畢氏定理道逆定理(即三條邊嘅值乎合公式)嚟證咁個三角形係一個直角三角形。

12.6.2.  畢氏定理與三角比的關係

其實除咗要證明一個三角形係直角三角形之外，所有畢氏定理計到嘅數都可以用三角比嚟計。方法如下：

• 先利用已知嘅兩條邊嚟計出其中一隻角。
• 利用其他三角比函數嚟計未知嘅第三條邊。