12. 演繹推理幾何 > 與多邊形有關的定理

12.7. 與多邊形有關的定理

與多邊形有關的定理 其實得兩條，如下圖：

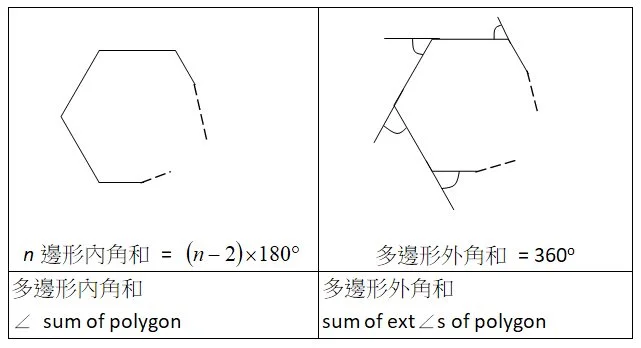
雖然多邊形嘅問題一般唔會太難，但同學可能被”唔知有幾多邊條”嚇親而往往表現未如理想。另一方面可能因為少做，所以唔記得有公式。其實只要明白依兩條定理係點得嚟嘅，到時“做”返條式出嚟都唔係好難。

• 解拆 n邊形內角和公式
  • 大家先喺紙度劃一個五邊形
  • 由其中一個頂點度劃直線到其他頂點度。
  • 每劃一條線，同學就應該見到多咗一個三角形。
  • 最終應分割到四個三角形出嚟。
  • 每一個三角形嘅內角和係180^o，所以五邊形內角和係
    3 x 180^o = 540^o
    只要你記得個3係“5 – 2”，即係“邊的數量 減 2”，你就會記得：

\( n邊形內角和 = (n – 2) \times 180^{\circ} \)

• 解拆 n邊形外角和
  • 對於一個n邊形嚟講，因為有n條邊，所以有“n個直線上的鄰角”。
  • 多邊形外角和
    = (n個直線上的鄰角) – (n邊形內角和)
    \(= n \times 180^{\circ} – (n – 2) \times 180^{\circ} \)
    \( = 180^{\circ}n – 180^{\circ}n + 360^{\circ} \)
    \( = 360^{\circ} \)

12.7.2.  平行四邊形

平行四邊形其實大家由細都識，只係無好認真咁去理解過。

大家要識嘅就係：

• 平行四邊形對邊長度相等而且平行。
• 平行四邊形嘅對角線互切。
  所謂互切就係指一條對角線會將另一條對角線切成兩等份（即長度相等）。
• 菱形嘅兩條對角線是垂直嘅。
  （註：菱形係一個四條邊都相等或內角唔等於90度嘅四邊形）。