12. 演繹推理幾何 > 全等三角形

12.4.  全等三角形 (Congruent Triangles)

講 全等三角形 ，首先當然要講吓個定義…

• 全等
  • 指兩個圖形嘅形狀同大小都完全相同。
  • 一個圖經平移、反射或旋轉變換後，可得一個同原來圖形全等嘅圖形。

全等 嘅符號係 \(\cong\)

• \(\triangle ABC 與 \triangle XYZ 全等 可寫成 \triangle ABC \cong \triangle XYZ \)

12.4.1 全等三角形性質

當兩個△全等時：

• 兩個△嘅對應邊 (corresponding sides) 相等，
• 兩個△嘅對應角 (corresponding angles) 相等。

12.4.2  全等三角形的條件

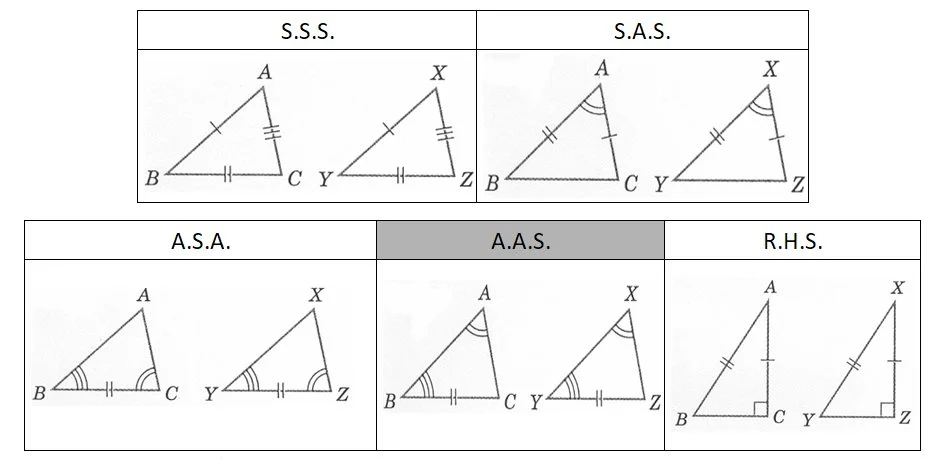
明白咗上面嘅基本嘢之後，我地更加緊要嘅係知道幾時兩個三角形先係全等。下面幅圖已總結咗全等嘅條件：

上面條件簡寫中，

• A係代表角
• S係代表邊
• R係代表直角
• H係代表斜邊

所為 “A.S.A.”係指兩個三角形“連續的角、邊、角”都係相等。

12.4.3.  寫全等三角形要留意的地方

• 我哋一定要依照對應角嘅位置寫出兩個全等△。
  在上面全等三角形條件圖中，\(\triangle ABC \cong \triangle XYZ\) ，我地唔可寫作 \(\triangle ABC \cong \triangle YXZ\)
• S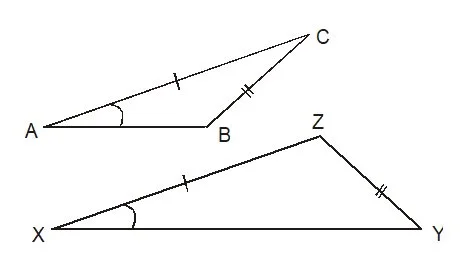SA不能用作證明全等△。
  睇吓右邊兩個△就知道佢哋 “唔全等”。
• A.A.S.係一個全等嘅條件，但我覺得可以不記。
  • 原因係如果兩個△嘅兩隻角都相等，利用△內角和，我哋可以證明到第三隻角都相等。
    咁我哋就可以利用“A.S.A.”嚟證明兩個△係全等嘅。