11. 坐標 > 坐標系統
11.1 坐標系統 (Coordinates System)
喺DSE入面，我地要學兩個 坐標系統，分別係
- 直角坐標 (Cartesian Coordinate)
- 極坐標 (Polar Coordinate)
11.1.1. 直角坐標 (Cartesian Coordinate)
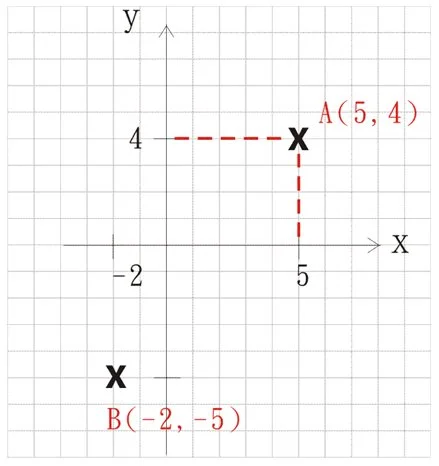右面幅圖就係我哋最常用嘅直角坐標系統。一般題目冇指明，我哋所見所用嘅都係直角坐標。
對每一點嚟講，我哋只要知佢嘅x-坐標同y-坐標就可以知道佢嘅位置。依組“x-坐標同y-坐標”就係叫“坐標”。
例1： 在右圖中，
- A點 = (5, 4)
- B點 = (-2, -5)
11.1.2. 極坐標 (Polar Coordinate)
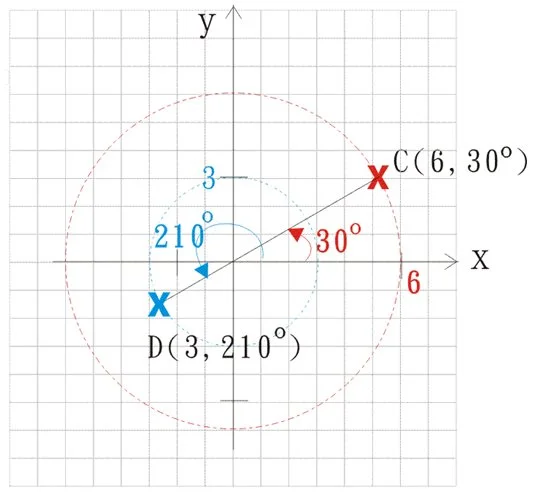“極坐標”喺我地另一個要識嘅坐標系統。用極坐標嘅時候，題目會講到明用緊極坐標。
留意喺極坐標度，括號入面一個係數字，一個係度數。
- 個數字係代表嗰點同原心點嘅距離（即圓半徑）
留意我哋可以想嗰點係喺一個圓形嘅周界上面。 - 個度數係代表方向，由x-軸逆時針方向量度起
例2：在右圖中，
- C點 = (6, 30°)
- D點 = (3, 210°)
11.1.3. 轉換坐標系統
- 喺DSE入面，同學最好學埋點樣將直角坐標同極坐標互換。
- 其實唔難，只要將個坐標劃出嚟，再利用簡單嘅三角比(即sin,cos等)就可以做到。
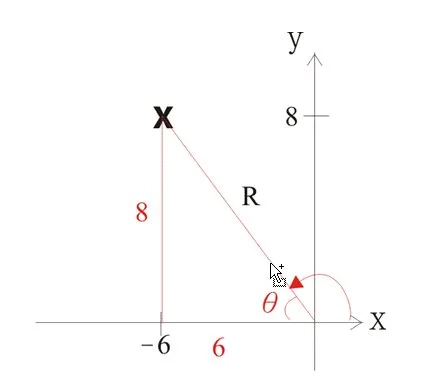例3： 已知A點的直角坐標為(-6, 8)。求A點的極坐標。
解答： 首先用直角坐標劃出A點（如右圖）。再劃出圖中的紅線以幫助我們求得極坐標。
利用畢氏定理，
\(R = \sqrt{6^{2} + 8^{2}} = 10 \)
利用三角比，
\(\begin{align}
tan \theta & = \dfrac{8}{6} \\
\theta & = 53.13^{\circ}
\end{align}\)
留意極坐標所用嘅角喺由x-軸開始，逆時針度起。
所以A點的極坐標為(10, 126.87°)。
例子4： 已知A點的極坐標為(10, 126.87°)。求A點的直角坐標。
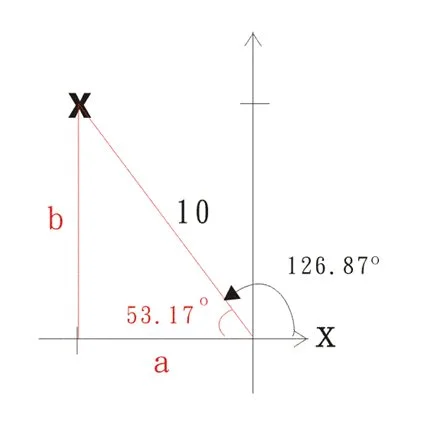解答： 首先把極坐標劃出（如右圖）。再劃出圖中的紅線以幫助我們求得直角坐標。
利用三角比，
\(\begin{align}
sin53.17^{\circ} & = \dfrac{b}{10} \\
b & = 8 \\
cos53.17^{\circ} & = \dfrac{a}{10} \\
a & = 6
\end{align}\)
留意極坐標係喺第二象限入面，x-坐標為負數。
所以A點的直角坐標為(-6, 8)。