11. 坐標 > 直線的斜率

11.3. 直線的斜率 (Slope of Straigt Lines)

11.3.1. 計算直線的斜率

\(AB的斜率 = \dfrac{y_{2} – y_{1}}{x_{2} – x_{1}} \)

我哋通常用細楷“m”代表斜率，所以AB的斜率通常會寫成  \(m_{AB}\)（留意AB係寫細D喺m嘅右下角）。

另外睇返幅圖，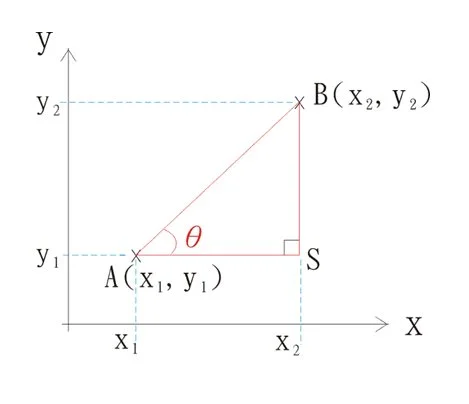

我希望你會接受到 斜率 係同個角度 θ 有關。利用三角比所學嘅嘢，應該不難發現：

\(\begin{align}
\dfrac{y_{2} – y_{1}}{x_{2} – x_{1}} = \dfrac{BS}{AS} = tan \theta \\
\therefore，\quad \quad AB的斜率 = tan \theta \)
\end{align}\)

13.3.2.  平行線與垂直線的斜率的關係

• 假設有兩條直線，它們的斜率分別係m₁同m₂。
  • 如果兩條線互相平行，則它們的斜率相等，即 \(m_{1} = m_{2} \)
  • 如果兩條線互相垂直，則 \(m_{1} \times m_{2} = -|\)