以圖像法解二次方程
1.3. 由繪畫拋物線的圖像及讀取該圖像的x截距解方程ax2+bx+c=0（Solve the Equation ax2+bx+c=0 by Plotting the Graph of the parabola and Reading the x-Intercepts）
DSE課程叫依部份做”由繪畫拋物線的圖像及讀取該圖像的x截距解一元二次方程”, 其實即係用 圖像法 解二次方程。
1.3.1. 繪畫 y=ax2+bx+c的圖像（Plotting the Graph of y=ax2+bx+c）
其實無論畫咩數學方程式嘅圖像，我哋都係用同一個技巧！步驟如下：
- 先畫一個表：
- 代唔同嘅x值入條式度計返相應嘅y值，再把數值填入表中。
- 例：如要畫 \(y = x^2 – x – 6\) 嘅圖像，個表最終會變成咁：
- 每一對x、y嘅值係代表圖像會經過嘅一點，例如圖像會經過點(-3, 6)。
- 暫時先唔好問點解x嘅值係由-3開始，然後不斷加1加到5。
- 例：如要畫 \(y = x^2 – x – 6\) 嘅圖像，個表最終會變成咁：
- 喺格仔紙（graph paper）度畫x軸同y軸出嚟。
- 留意x軸嘅“長度”至小要由-3去到5，y軸嘅“長度”就至小要由-6去到14。
- 留意x軸嘅“長度”至小要由-3去到5，y軸嘅“長度”就至小要由-6去到14。
- 將個表入面嘅點標記落格仔紙度。
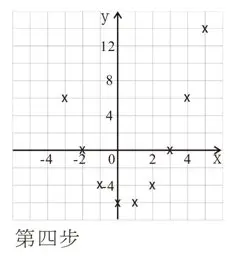
- 最後畫一條“曲線”將D點連埋一齊。
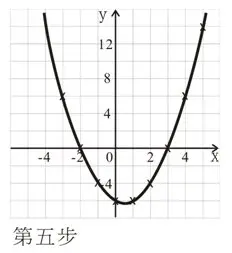
圖像就畫完喇，不過大家要留意以下幾點：
- 首先，大家係唔駛理課程中提到嘅“拋物線”。總之你太約知道畫出嚟嘅唔係直線，而係一條曲線，個樣好似一隻碗咁就得嫁喇。
- 喺公開試度大家應該係唔駛畫曲線嘅！
- 原因係太花時間同好難定個評分標準（例如大家冇可能畫到條好“靚”嘅曲線，同埋x值嘅範圍要攞幾多先啱呢？）
- 不過大家喺學校嘅測驗、考試就唔同講法。（教嘅嘢唔多嘅時候，老師都可能都會出畫圖題。）
1.3.2. 讀取y=ax2+bx+c的圖像的x截距解方程（Solve the Equation ax2+bx+c=0 by Reading the x-Intercepts）
§ 其實依節 圖像法 要學嘅嘢已經喺上面個標題教咗。
- 舉個例嚟講。先假設我哋已經有\(y = x^2 – x – 6\)嘅圖像（即係我哋喺前面個課度畫嘅圖）。
- 如果題目要求我哋去解一元二次方程\(x^2 – x – 6 = 0\)，其實我哋要做嘅只係睇返圖像嘅x截距就已經可以知邊方程嘅根。
- 唔信嘅可以試一次：
\(\begin{align}
& x^2 – x – 6 = 0 \\
& (x -3)(x + 2) = 0\\
& x – 3 = 0 \quad 或 \quad x + 2 = 0\\
& x = 3 \quad 或 \quad x = -2
\end{align}\) - 睇睇右圖，方程\(x^2 – x – 6 = 0\)嘅兩個根（即係3同-2）嘅值就係圖像嘅x截距。
要學嘅就係咁多，不過我覺得最好都明白吓當中嘅原因。咁會幫到大家清concept：
- 首先最重要嘅concept係如果個圖像經過一點(k, m) （k同m可以係數字或者係未知數），咁即係話我哋可以代依點入去圖像嘅數式度（即係可以代入去 \(y = x^2 – x – 6\)）。
- 所以我哋可以得到 \(m = k^2 – k – 6\)。
- 就咁睇好似冇咩特別。不過如果我哋當幅圖會經過(k, 0)，咁即係話：
\(0 = k^2 – k – 6\)
即 \(k^2 – k – 6 = 0\)- 如果我哋唔理以前做過D咩，只係睇住\(k^2 – k – 6 = 0\)。咁我哋又可以話搵到一個數值“k”可以令到方桯 \(x^2 – x – 6=0\) 成立 （即係 k 係方程嘅根）。
- 咁到底k又係幾多呢？
- 因為之前已經話 \(y = x^2 – x – 6 \)嘅圖像會經過(k, 0)。
- 而(k, 0)又係幅圖嘅x截距。
- 所以我哋會話： “讀取 \(y=ax^2+bx+c\) 圖像嘅x截距可以解方程 \(ax^2+bx+c=0\)”