二次函數圖像
2.3 理解 二次函數圖像 的特徵 (Understand the Features of the Graphcs of Quadratic Functions)
2.3.1 二次函數圖像的特徵
學 二次函數圖像 (即 y = ax2 + bx + c 嘅圖像),首先當然要知佢個樣。 二次函數圖像個樣係好似一隻碗咁(就好似下面幅圖嘅紅線咁):
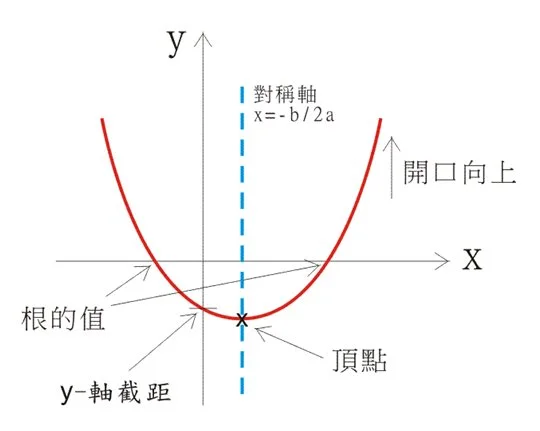
§ 睇幅圖嘅時候,我哋要留意:
- 開口方向,即開口係向上定向下。
- 上圖中二次函數圖像嘅開口係向上的。
- y-軸截距係正定負
- 上圖中二次函數圖像嘅y-軸截距係負的。
- ax2 + bx + c=0嘅根嘅值及數目
- 從 y = ax2 + bx + c 的圖像中, ax2 + bx + c=0嘅根係曲線與 x-軸同交的點。
- 從上圖可見方程有兩個實根,一正一負。
- 對稱軸(axis of symmetry)嘅位置
- 上圖中嘅對稱軸係 “喺正嗰邊”。
- 所以幅圖一大半係喺y-軸右邊
- 上圖中嘅對稱軸係 “喺正嗰邊”。
- 頂點(vertex)嘅坐標
- 如果開口向上,咁個頂點就係二次函數嘅“極小值”(maximum value)。
- 如果開口向下,咁個頂點就係二次函數嘅“極大值”(minimum value)。
2.3.2 二次函數圖像的特徵與系數的關係
知道咗二次函數圖像的特徵後,我地要學嘅係點樣從題目俾你嘅函數(如y = x2 + 5x + 1)嚟決定個圖嘅樣。
- HKDSE 數學卷二 (MC卷) 好鐘意考依個concept。
- 題目係好可能會俾個圖你,問你a、b同c係正定負。
做依類題目嘅技巧係要明白“a、b同c點影響圖樣嘅樣”:
- a > 0 即開口向上。
- a < 0 即開口向下。
- c = y-軸截距
- 因當x=0時,代入函數可得 y = a(0)2 + b(0) + c = c
- 如果b2 – 4ac > 0就有兩個根
- 個圖會穿過x-軸兩次
- 如果b2 – 4ac = 0就有一個根
- 個圖只會掂到x-軸一次
- 如果b2 – 4ac < 0就冇實根
- 個圖唔會掂到x-軸
- 即係要計或判斷 –b/2a 嘅值係正定負
- 如果 –b/2a > 0即係對稱軸喺y-軸嘅右邊,個圖會靠右。
- 如果 –b/2a < 0即係對稱軸喺y-軸嘅左邊,個圖會靠左。
- 又或者從圖像中對稱軸係喺正嗰邊定喺負嗰邊,再加上已知 a 嘅正負嚟決定 b嘅正負
- 頂點嘅坐標可以直接睇圖。
- 如果要計就用以下方法:
- 頂點嘅x坐標 = -b/2a (即係對稱軸嘅位置)
- 有咗“頂點嘅x坐標”之後,可以代入函數計相應嘅y值。
完依一章節之前,我地睇一個例子。
分析:
- a < 0
- 所以開口向下
- x=0時,y = -7
- 所以y-軸截距 = -7
- b2 – 4ac = (5)2 – 4(-1)(-7) = -3 < 0
- 所以沒有根,即圖像不會與x-軸相交。
- –b/2a = – (5) / 2(-1) = 2.5 > 0
- 所以對稱軸在y-軸的右邊
* 知道以上幾點之後就可以劃到“隻碗”出嚟
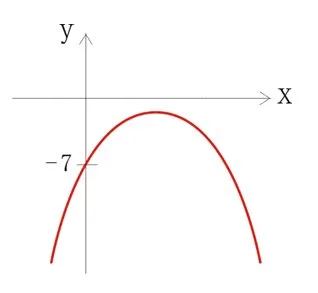
(公開試係唔會叫你劃曲線嘅,依個例子只係想你明白D道理。)
