軌跡的代數方程
12.1 以代數方程描述點的軌跡 (Describe the Locus of Points with Algebraic Equations)
前面已講咗軌跡嘅概念。但當中並冇提及 軌跡的代數方程 。
- 而依一課學嘅就係要學點搵 軌跡的代數程
喺數學上,一個軌跡其實通常係一條代數方程。而求依條方程嘅方法多數係:
- 想像喺軌跡上面有一點(x,y)(依點就係我哋之前提到喺軌跡上隨意走動嘅點)。
- 然後將軌跡要乎合嘅“條件”用數學嘅方法表達出嚟(即係列條數式出嚟)。
- 最後將列出嚟嘅數式化簡。
§ 軌跡嘅問題可以話千變萬化。不過幸好依個課題只係必俢部份、仲要喺基礎課題。所以應該唔會考得太深同變得大離譜。
- 根據課程,大家要識嘅係“求簡單軌跡的方程”,包括:
- 直線
- 圓
- 形式如 y = ax2 + bx + c 的拋物線
- 但按 DSE Maths Paper Paper 嘅題目嚟睇, 要你搵拋物線嘅軌跡 (Locus)嘅機會係微乎其微。
12.3.1. 求直線軌跡的方程
直線離有以下三種:
- 水平線
- 方程個樣係 y = k (k為常數)。
- 例子: y = 3。
- 鉛垂線
- 方程個樣係 x = k (k為常數)。
- 例子: x = 5。
- 斜線。
- 方程個樣係 ax + by + c = 0 (a, b, c為常數)。
- 例子: 2x + y + 3 = 0。
如果要求嘅軌跡係一條水平線或鉛垂線,其實只要理解題目,咁就條數係唔多駛計嘅。
解說:先想一想個軌跡會係咩樣。
- 照計大家應該可以諗到答案會係一條喺y = 3 同 y = 7日間嘅水平線。
(睇唔到就畫 y = 3 同 y = 7 出嚟) - 所以P點的軌跡是 y = 5。
解說:先想一想個軌跡會係咩樣。
- 照計大家應該可以諗到答案會係一條兩點之間嘅鉛垂線。
- 所以Q點的軌跡是 x = 6。
如果要求嘅軌跡係一條斜線,咁就多數要“計一計”。
解說:先想一想個軌跡會係咩樣。
- 留意兩條線嘅方程只係最後嘅數字唔同。咁係代表兩條線係平行線。
- 照計大家應該諗到個答案會係喺佢哋中間嘅平行線。而條線嘅方程同佢哋都係差唔多樣,只係最後嘅數字會等於“3同9”嘅平均數。
- 所以R點的軌跡是 3x + y + 6 = 0。
解說:先想一想個軌跡會係咩樣。
- 如果你以為答案係一條水平或鉛垂線,就唔該畫一畫兩點同個“你想到嘅答案”出嚟。(留意今次嘅題目入面嗰兩點嘅x、y-坐標都係唔同嘅。)
- 要搵個答案,我哋要用最初有提咗嘅“將軌跡要乎合嘅條件用數學嘅方法表達出嚟”嘅方法:
- 設S點為 (x, y)。
- SA長度 = SB長度
(x – 4)2 + (y – 5)2 = (x – 8)2 + (y – 1)2
x2 – 8x + 16 + y2 – 10y + 25 = x2 – 16x + 64 + y2 – 2y + 1
– 8x + 16 – 10y + 25 = – 16x + 64 – 2y + 1
8x – 8y – 24 = 0
x – y – 3 = 0
以上我哋用咗初中坐標幾何入面學過嘅兩點距離公式。唔記得嘅可以睇睇“唔好以為唔駛考課題”入面嘅教程。
至於角平分線嘅軌跡(即12.2.6入面話嘅軌跡)我就覺得應該唔會出。
- 咁喺因為好似課程入面冇提到要大家識得計“一點與一條直線嘅距離”(喺HKCEE會考入面依個係附加數嘅課題)。
12.3.2 求圓軌跡的方程
- 如果題目要求嘅軌跡係“有一點同另一固定點保持固定距離”嘅話,咁個軌跡就係一個圓形。依個時候我哋又係要用“將軌跡要乎合嘅條件用數學嘅方法表達出嚟”嘅方法。
解說:個軌跡好明顯係一個圓。
- 設S點為 (x, y)。
- SA長度 = 3
(x – 4)2 + (y – 5)2 = 9
x2 – 8x + 16 + y2 – 10y + 25 = 9
x2 + y2 – 8x – 10y + 32 = 0
到底點解上面嘅方程係一個圓形大家可能唔明。
- 先接受吧!我哋會喺“第13課 – 直線與圓的方程”度學圓嘅方程。
12.3.3 求拋物線軌跡的方程
正如個名所講,“拋物線軌跡”喺當我哋拋一個物體出去之後,佢所走嘅路線嘅樣。
- 數學上佢其實就係我哋學過嘅一元二之方程圖像(即y = ax2 + bx + c)。
- 現實生活中嘅拋物線當然要係“個圖像嘅開口向下”。
- 而“拋物線軌跡”所乎合的條件是“有一點與一固定點及直線的距離係相等的”。
其實當大家睇唔到個軌跡係咩而用“軌跡要乎合嘅條件用數學嘅方法表達出嚟” 嘅時候,我哋可以唔駛理個軌跡係咩。只要跟住個方法照做:
- 設P點為 (x, y)。
- P點與點A(2,1)的距離 = P點與直線y=1的距離
\(\begin{align}
\sqrt{(x-2)^{2}+(y-3)^{2}} &= y-1 \\
(x-2)^{2}+(y-3)^{2} &= (y-1)^{2} \\
x^{2}-4x+4+y^{2} -6y+9 &= y^{2}-2y+1 \\
x^{2} -4x+13 &= 4y+1 \\
4y &= x^{2}-4x+12 \\
y &= \tfrac{1}{4}x^{2}-x+3
\end{align}\)
最終軌跡嘅圖像如下:
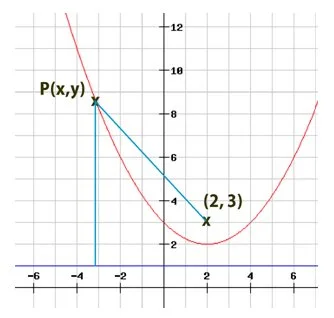
- 留意P點與直線y=1的距離係條鉛垂線,長度 = y – 1。
