我發現不少覺得DSE數學困難的同學其實其數學理解或能力未必一定係好差,反而好多時候只係因為唔知點入手而做唔到題目。喺度我教大家其中一個 DSE數學解題技巧, 主要針對大家嘅思維方法……
唔好以為可以直接計到個答案!!!
要改為問自己還欠什麼才可以計到答案!!
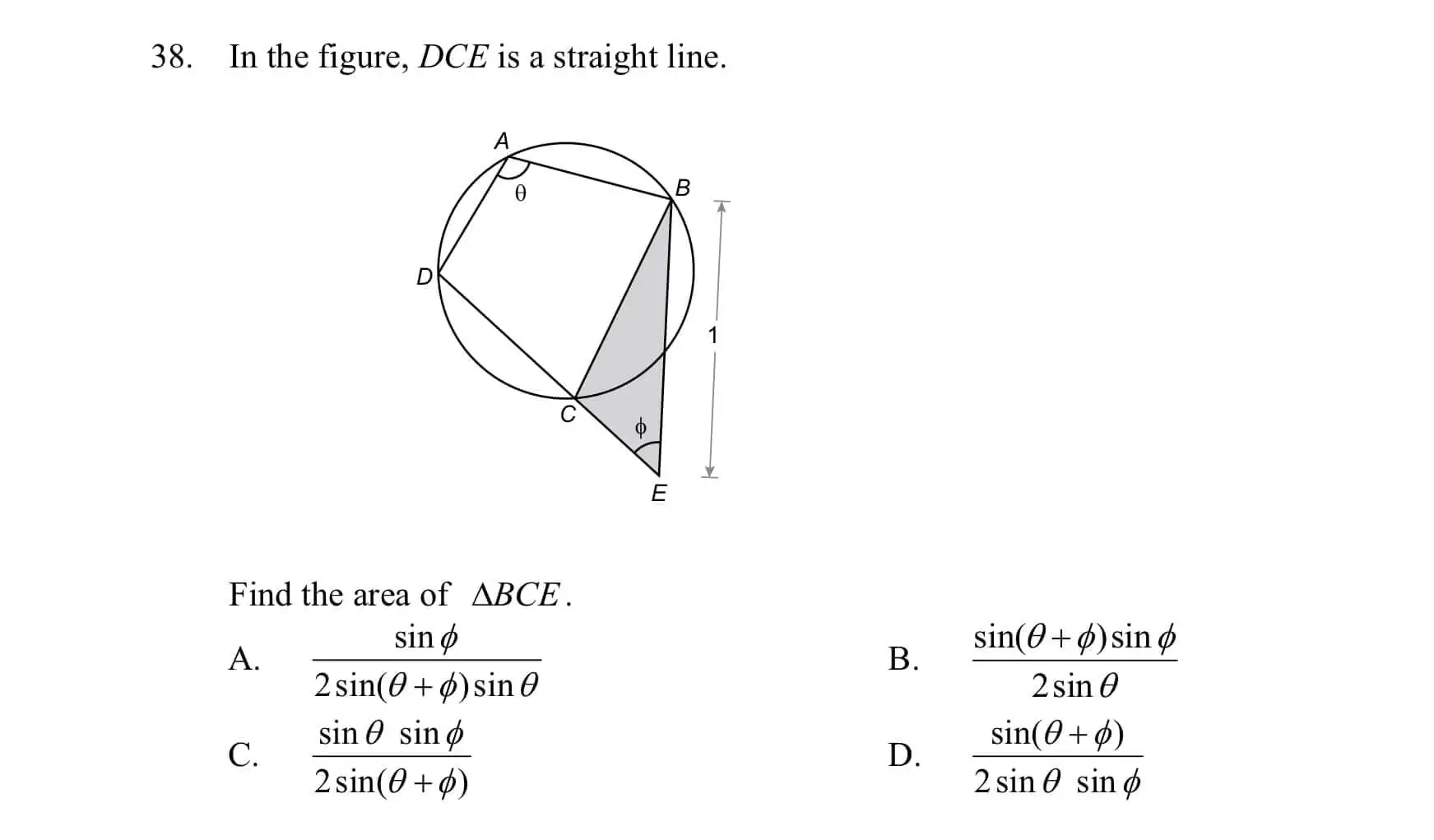
有感而發主要係因為剛在Facebook看到有人問一條MC題目。題目是涉及與圓形有關的幾何學。但跟一般的問題不同,這題不是叫你去計某一角的大小,而是要去計算一個三角形的面題。題目比較特別,可能也是因為咁同學做唔到而上網求救。
如果同學只係一路係咁諗點先計到個三角形面積,咁好能會浪費不少時間。計算三角形面積。絕大部份的同學都應知”三角形面積 = 底 x 高 / 2″。而喺DSE課程中,我哋亦學咗 “三角形面積 = (1/2) ab sinθ”。
因此,在我地不能直接求得三角形面積時 (因為如BE係底, 咁我地唔知個高係幾多),我地要先問自己點先計到個 高 或 線段CE的長度。而這也可說是題目真正要考大家嘅嘢。
而係計算線段CE的長度,我地可以先睇吓題目比嘅咩資料我地 (因為題目所比的資料,理論如果唔用係計唔到條數的)。而題目比咗個有囻內接四邊形嘅圖我地,我地可以先用一用佢:
∠BCE = ∠DAB = θ (ext ∠, cyclic quad. | 囻內接四邊形外角)
去到這裡,我地已經知道ΔBCE中3條邊和3隻角的其中三個,所以理應可以用sine formula (正弦公式) 或 consine formula (餘弦公式)去求其餘的邊和角。但當然在這裡,我地只需要去計CE。
利用sine formula,
\(\begin{align}
\dfrac{CE}{sin ∠CBE} &= \dfrac{BE}{sin ∠BCE} \\
\dfrac{CE}{sin (180° – (\theta + \phi))} &= \dfrac{1}{sin\theta} \\
CE &= \dfrac{sin(\theta + \phi)}{sin\theta} \\
\\
\therefore, \text{area of }ΔBCE &= \dfrac{1}{2} (CE) (BE) sin\phi \\
&= \dfrac{1}{2} \times \dfrac{sin(\theta + \phi)}{sin\theta} \times sin\phi
\end{align}\)
故答案為 B。
如大家都溫習返相關課程內容, 可以睇返