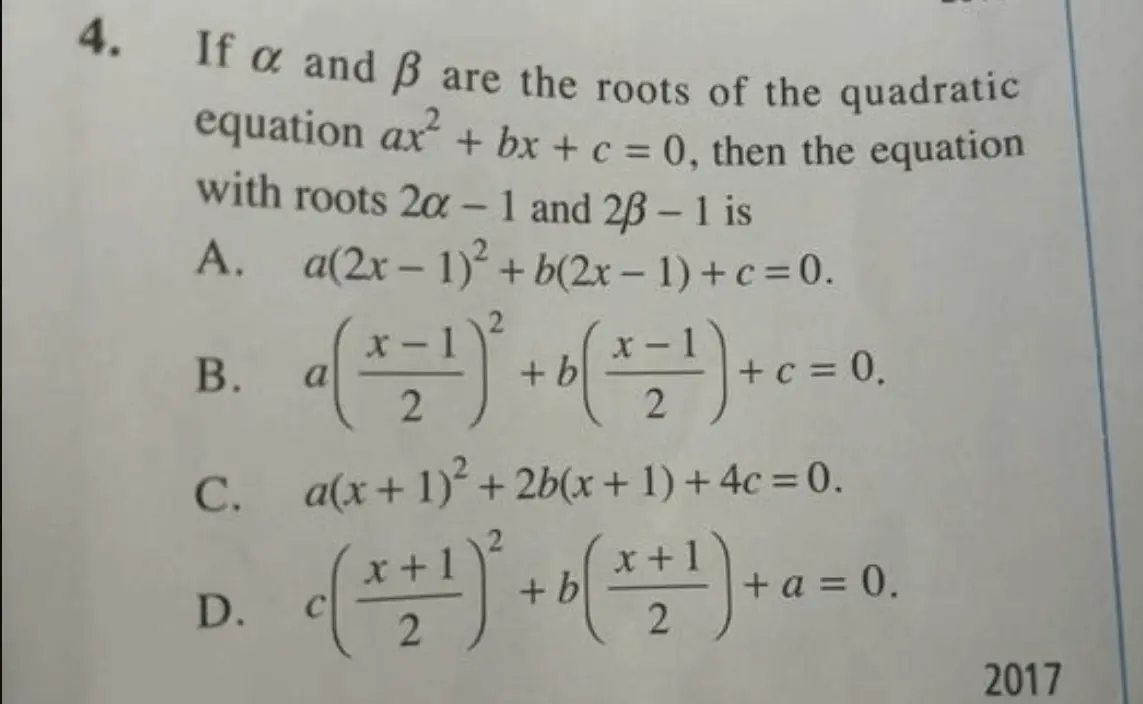α今日在臉書上看到有同學發問一條一元二次方程的題目。題目本身不算十分難, 但要計到答案其實有一個”快方法”。這令我不禁問坊間的補習社老師不少都標榜自己有好多獨問秘技, 但到底這些秘技到底幫唔幫到手呢? 這值得我們去思想一吓….
要做這條題目, 一個比較快的方法如下:
因為新方程根為 2α – 1 及 2β – 1, 故設 y = 2x – 1。即
\(x = \dfrac{y+1}{2}\)
要求的方程為:
\(\begin{align}
a (\dfrac{y+1}{2})^{2} + b (\dfrac{y+1}{2}) + c &= 0 \\
a (y+1)^{2} + 4b(\dfrac{y+1}{2}) + 4c &= 0 \\
a (y+1)^{2} + 2b(y+1) + 4c &= 0 \\
\end{align}\)
留意一條方程的變數係x定係y並不影響到根的值, 故答案為C。
以上的方法一般老師都未必會講解, 就算有用都未必會詳細解釋。對數學好的同學來說的確可以說是學到一技新嘅秘技。但對數學唔好嘅同學, 考試時佢地都好可能未必想起可以用這秘技。
不如我地又睇吓如果用”傳統”手法去做, 依條題目會點做。首先, 因為題目係要求一條以新的根的方程, 我地先要計舊方程的 sum of roots (根之和) 及 product of roots (根之積)。
α + β = -b/a
αβ = c/a
現考慮新方程,
\(\begin{align}
sum of roots &= (2\alpha – 1) + (2\beta – 1) \\
&= 2(\alpha + \beta_ – 2 \\
&= \dfrac{-2b}{a} – 2 \\
product of roots &= (2\alpha – 1) \times (2\beta – 1) \\
&= 4\alpha \beta – 2(\alpha + \beta) + 1 \\
&= \dfrac{4c}{a} + \dfrac{2b}{a} + 1 \\
&= \dfrac{4c + 2b+ a}{a}
\end{align}\)
所以要求的方程為:
\(\begin{align}
x^{2} +(\dfrac{2b}{a} + 2)x + (\dfrac{4c + 2b+ a}{a}) = 0 \\
ax^{2} +(2b + 2a)x + (4c + 2b+ a) = 0 \\
a(x^{2} + 2x + 1) + 2b(x + 1) + 4c = 0 \\
a(x + 1)^{2} + 2b(x + 1) + 4c = 0
\end{align}\)
當然，答案也是C。
另一個可行的”快”方法是
- 先設原方程為 \(x^{2} + 4x + 3 = 0\), 即 a=1, b=4, c=3。而根為 -3和-1。
- 新方程的根為 x = -7 和 x = -3。
- 最後把 -7, -3代入各選項中的方程, 左邊的值應為0, 否則會不是是答案。
