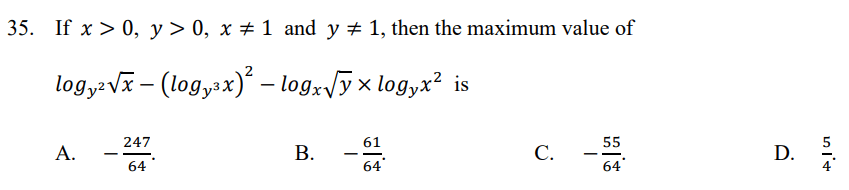喺面對唔識做嘅數學題目時,到底有咩 解題技巧 ?
- 首要唔好慌、唔好被題目嚇親。
- 其次,冷靜咁睇一次條題目,試吓從題型或關鍵字眼嚟估吓條題目其實係想考你邊一課嘅數學技巧。
知道題目想考你咩,其實往往係解題嘅關鍵…..
好似依條題目咁,我喺Facebook 中學數學功課交流區 度見到有人發問。就咁一睇,好可能好多同學都唔知要點做。但只要冷靜睇題目,我地應會留意到題目所問的涉及到以下課題及技巧:
- maximum value
這令我想起了一元二次方程中找最大值的方法… 配方法 (Completing square) - 對數
特別題目中有 logab 出現。故係要用到公式:
\(log_{a}b = \dfrac{log b}{log a}\)
有了這念頭便可開始化簡題目中的數式….
\(\begin{align}
&log_{y^{2}}\sqrt{x} – (log_{y^{3}} x)^2 – log_{x}\sqrt{y} \times log_{y}x^{2} \\
&= \dfrac{log x^{1/2}}{log y^{2}} – (\dfrac{log x}{log y^{3}})^{2} – \dfrac{log y^{1/2}}{log x} \times \dfrac{log x^{2}}{log y} \\
&= \dfrac{\tfrac{1}{2}log x}{2 log y} – (\dfrac{log x}{3log y})^{2} – \dfrac{\tfrac{1}{2}log y}{log x} \times \dfrac{2log x}{log y} \\
&= \dfrac{1}{4}\dfrac{log x}{log y} – \dfrac{1}{9}(\dfrac{log x}{log y})^{2} – 1 \\
&= -\dfrac{1}{9}z^{2} + \dfrac{1}{4}z – 1 \quad \quad (where z = \dfrac{log x}{log y}) \\
&= -\dfrac{1}{9} [z^{2} – \dfrac{9}{4}z] – 1 \\
&= -\dfrac{1}{9} [(z – \dfrac{9}{8})^2 – (\dfrac{9}{8})^{2}] – 1 \\
&= -\dfrac{1}{9} (z – \dfrac{9}{8})^2 + \dfrac{9}{64} – 1 \\
&= -\dfrac{1}{9} (z – \dfrac{9}{8})^2 – \dfrac{55}{64}
\end{align}\)
留意一個數嘅二次方最細為0, 所以上面嘅數式最嘅嘅值就係 -55/64。