問題: 平面幾何 – 圖形面積比 (DSE MC棘手題型)

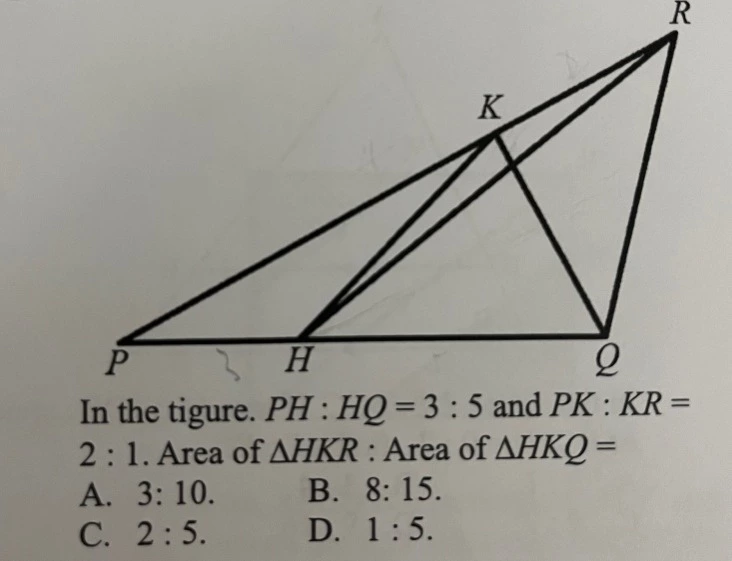
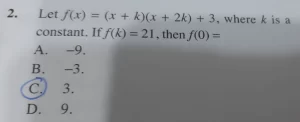有同學在Facebook發問了一條幾何學中有關面積比的題目 (詳見: https://www.facebook.com/groups/1187564858047414/posts/2883904991746717/ )

這題目其實在每年DSE數學MC卷中都會出現。因為圖形次次不同，縱使同學懂得計算面積比的技巧，但還是有機會要花上一點時間才能計出正確答案。大家平日可次做的，就是簡中做一做這題型的題目。到實戰時遇上困難，大可先把該問題擱下，先做其他的題目。稍後有時間時再回來做。

好了, 以下是這題的解題要點/過程。

• 留意題目提供了PH: HQ。而PH正是ΔPHK的一條邊。
  • 我們因此先計出ΔHKR與ΔHKP的面積比。
  • 把PH、HQ看到為兩個三角形的底，而它們的高是相等的(高為由K點劃一垂直線到PQ)。因此
    • ΔPHK : ΔHQK = 3 : 5
• 留意題目亦提供了PK: KR。而KR正是ΔHKR的一條邊。
  • 用同一手法，把PK、KR看到為兩個三角形的底，而它們的高是相等的(高為由H點劃一垂直線到PR)。因此
    • ΔHKR : ΔPHK = 1 : 2

到這刻，題目就變成了:

• 已知 a : b = 1 : 2，b : c = 3: 5。求 a: c
• a : b      = 1 : 2 = 3 : 6
        b: c = 3: 5 =        6: 10
• 因此，a : c = 3 : 10。

答案為A